Câu 10: Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q (h.9)
Chứng minh rằng MN = PQ.
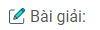
Trong tam giác ADB, ta có: MN // AB (gt)
Suy ra: \({{DN} \over {DB}} = {{MN} \over {AB}}\) (Hệ quả định lí Ta-lét ) (1)
Trong tam giác ACB, ta có: PQ // AB (gt)
Suy ra: \({{CQ} \over {CB}} = {{PQ} \over {AB}}\) (Hệ quả định lí Ta-lét ) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong tam giác BDC, ta có: NQ // CD (chứng minh trên)
Suy ra: \({{DN} \over {DB}} = {{CQ} \over {CB}}\) (Định lí Ta-lét ) (3)
Từ (1), (2) và (3) suy ra: \({{MN} \over {AB}} = {{PQ} \over {AB}}\) hay MN = PQ.
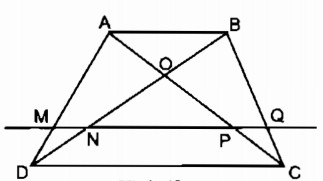
Câu 11: Cho hình thang ABCD (AB // CD). Trên cạnh bên AD lấy điểm E sao cho \({{AE} \over {ED}} = {p \over q}\) . Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F
Chứng minh rằng: \(EF = {{p.CD + q.AB} \over {p + q}}\)
HD: Kẻ thêm đường chéo AC, cắt EF ở I, rồi áp dụng hệ quả định lí Ta-lét vào các tam giác ADC và CAB.
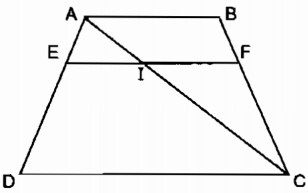
Kẻ đường chéo AC cắt EF tại I.
Trong tam giác AEC, ta có: EI // CD
Suy ra: \({{AE} \over {AD}} = {{EI} \over {CD}}\) (Hệ quả định lí Ta-lét )
Suy ra: \(EI = {{AE} \over {AD}}.CD\) (1)
Lại có: \({{AE} \over {ED}} = {p \over q}\) (gt)
Suy ra: \({{AE} \over {AE + ED}} = {p \over {p + q}}\)
Suy ra: \({{AE} \over {AD}} = {p \over {p + q}}\) (2)
Từ (1) và (2) suy ra: \(EI = {p \over {p + d}}.CD\)
Trong tam giác ABC, ta có: IF // AB
Suy ra: \({{BF} \over {FC}} = {{AI} \over {IC}}\) (Định lí Ta-lét ) (3)
Advertisements (Quảng cáo)
Trong tam giác ADC, ta có: EI // CD
Suy ra: \({{AE} \over {ED}} = {{AI} \over {IC}}\) (Định lí Ta-lét ) (4)
Từ (3) và (4) suy ra: \({{BF} \over {FC}} = {{AE} \over {ED}} = {p \over q}\)
Trong tam giác ABC, ta có: IF // BC
Suy ra: \({{IF} \over {AB}} = {{CF} \over {CB}}\) (Hệ quả của định lí Ta-lét)
Suy ra: \(IF = {{CF} \over {CB}}.AB\) (5)
Ta có: \({{BF} \over {CF}} = {p \over q}\) (cmt)
Suy ra: \({{CF} \over {BF}} = {q \over p} \Rightarrow {{CF} \over {CF + BF}} = {q \over {p + q}} \Rightarrow {{CF} \over {CB}} = {q \over {p + q}}\) (6)
Từ (5) và (6) suy ra: \(IF = {q \over {p + q}}.AB\)
Vậy: \(EF = EI + {\rm I}F = {p \over {p + q}}.CD + {q \over {p + d}}.AB = {{p.CD + q.AB} \over {p + q}}\)
Câu 12: Hình thang cân ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O (h.11). Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm.
a. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
b. So sánh độ dài đoạn thẳng MN với nửa hiệu các độ dài của CD và AB.
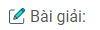
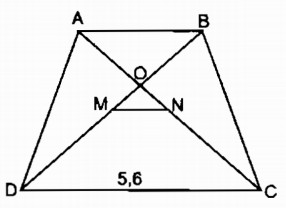
a. Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ∆ADC và ∆BCD, ta có:
AC = BD (chứng minh trên )
Advertisements (Quảng cáo)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: ∆ADC = ∆BCD (c.c.c)
Suy ra: \(\widehat {ACD} = \widehat {BDC}\)
Hay \(\widehat {OCD} = \widehat {ODC}\)
Suy ra tam giác OCD cân tại O
Suy ra: (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong tam giác OCD, ta có: \({{MO} \over {MD}} = {{NO} \over {NC}} = {1 \over 3}\)
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét )
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong tam giác OCD, ta có: MN // CD
Suy ra: \({{OM} \over {OD}} = {{MN} \over {CD}}\) (Hệ quả định lí Ta-lét )
Suy ra: \({{MN} \over {CD}} = {{OM} \over {4OM}} = {1 \over 4}\)
Suy ra: \(MN = {1 \over 4}CD = {1 \over 4}.5,6 = 1,4\) (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt), suy ra: MN // AB
Trong tam giác OAB, ta có: MN // AB
Suy ra: \({{OM} \over {OB}} = {{MN} \over {AB}}\) (Hệ quả định lí Ta-lét )
Suy ra: \({{MN} \over {AB}} = {{OM} \over {2OM}} = {1 \over 2}\)
Vậy AB = 2MN = 2.1,4 = 2,8 (cm)
b. Ta có: \({{CD – AB} \over 2} = {{5,6 – 2,8} \over 2} = {{2,8} \over 2} = 1,4\) (cm)
Vậy MN\( = {{CD – AB} \over 2}\)
Câu 13: Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm của các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng:
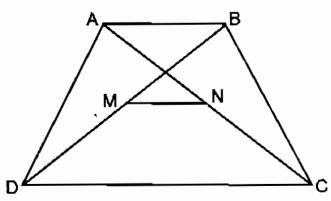
a. MN// AB;
b. \(MN = {{CD – AB} \over 2}\)
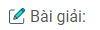
a. Gọi P là trung điểm của AD, nối PM.
Trong tam giác DAB, ta có:
\({{PA} \over {AD}} = {1 \over 2};{{BM} \over {BD}} = {1 \over 2}\)
Suy ra: \({{PA} \over {AD}} = {{BM} \over {BD}}\)
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong tam giác ACD, ta có: \({{AP} \over {AD}} = {1 \over 2};{{AN} \over {AC}} = {1 \over 2}\)
Suy ra: \({{AP} \over {AD}} = {{AN} \over {AC}}\)
Suy ra: PN // CD ( Định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
b. Vì PM là đường trung bình của tam giác DAB nên:
\(PM = {{AB} \over 2}\) (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ADC nên:
\(PN = {{AB} \over 2}\) (tính chất đường trung bình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = \({{CD} \over 2} – {{AB} \over 2} = {{CD – AB} \over 2}\)

