Câu 6: Cho tam giác ABC có cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N (h.5)
Tính theo a độ dài của các đoạn thẳng DM và EN.
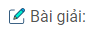
Ta có: AD = DE = EB = \({1 \over 3}AB\) (1)
Suy ra: AE = AD + DE = \({2 \over 3}AB\) (2)
Trong ∆ ABC, ta có : DM // BC (gt)
Nên \({{AD} \over {AB}} = {{DM} \over {BC}}\) (hệ quả định lí Ta-lét)
Suy ra: \({{AD} \over {AB}} = {{DM} \over a}\) (3)
Từ (1) và (3) suy ra: \({{DM} \over a} = {1 \over 3}\)
Suy ra: \(DM = {1 \over 3}a\)
Trong ∆ABC, ta có: EN // BC (gt)
Suy ra: \({{AE} \over {AB}} = {{EN} \over {BC}}\) (hệ quả định lí Ta-lét)
Suy ra: \({{AE} \over {AB}} = {{EN} \over a}\) (4)
Từ (2) và (4) suy ra: \({{EN} \over a} = {2 \over 3}\) hay \(EN = {2 \over 3}a\)
Advertisements (Quảng cáo)
Câu 7: Hình 6 chi biết MN // BC, AB = 25cm, BC = 45cm, AM = 16cm, AN = 10cm.
Tính độ dài x, y của các đoạn thẳng MN, AC.
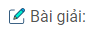
(xem hình 6)
Trong ∆ ABC, ta có: MN // BC (gt)
Suy ra: \({{AN} \over {AB}} = {{AM} \over {AC}} = {{MN} \over {BC}}\) (hệ quả định lí Ta-lét)
Suy ra: \({{10} \over {25}} = {{16} \over y} = {x \over {45}}\)
Vậy : \(y = {{25.16} \over {10}} = 40\)
Advertisements (Quảng cáo)
\(x = {{10.45} \over {25}} = 18\)
Câu 8: Hình 7 cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC và BC.
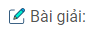
(xem hình 7)
Trong ∆ ABC ta có: MN // BC (gt)
Suy ra: \({{AM} \over {AB}} = {{AN} \over {AC}}\) (định lí Ta-lét)
Suy ra: \(AC = {{AB.AN} \over {AM}} = {{24.12} \over {16}} = 18\) (cm)
Vậy: NC = AC – AN = 18 – 12 = 6 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
\(\eqalign{ & M{N^2} = A{M^2} + A{N^2} = {16^2} + {12^2} = 400 \cr & MN = 20(cm) \cr} \)
Trong ∆ABC, ta có: MN // BC (gt)
Suy ra: \({{AM} \over {AB}} = {{MN} \over {BC}}\) (hệ quả định lí Ta-lét)
Vậy: \(BC = {{MN.AB} \over {AM}} = {{20.24} \over {16}} = 30\) (cm)
Câu 9: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O (h.8).
Chứng minh rằng: OA.OD = OB.OC.
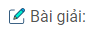
(hình 8 trang 84 sbt)
Trong ∆ OCD, ta có: AB // CD (gt)
Suy ra: \({{OA} \over {OC}} = {{OB} \over {OD}}\) (hệ quả định lí Ta-lét)
Vậy OA.OD = OB.OC.

