Câu 23: Cho tam giác ABC trong đó BC là cạnh lớn nhất.
a) Vì sao các góc B và C không thể là góc vuông hoặc góc tù?
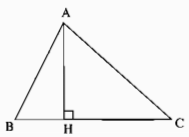
b) Gọi AH là đường vuông góc kẻ từ A đến BC. So sánh AB + AC với BH + CH rồi chứng minh rằng AB + AC > BC.
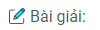
a) Giả sử \(\widehat B \ge 90^\circ\) => AC > BC
(Trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất)
Trái giả thiết cạnh BC là cạnh lớn nhất
Giả sử \(\widehat C \ge 90^\circ \) => AB > BC
(Trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất)
Trái với giả thiết BC là cạnh lớn nhất
Vậy \(\widehat B,\widehat C\) là các góc nhọn.
b) Ta có điểm H nằm giữa B và C => BH + HC = BC (1)
Ta có: AB > BH (đường xiên lớn hơn đường vuông góc)
AC > CH (đường xiên lớn hơn đường vuông góc)
Cộng từng vế ta có : B + AC > BH + CH (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: AB + AC > BC
Câu 24: Cho hai điểm A và B nằm về hai phía của đường thẳng d. Tìm điểm C thuộc đường thẳng d sao cho tổng AC + CB là nhỏ nhất.
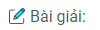
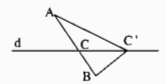
Gọi C là giao điểm của đoạn thẳng AB với đường thẳng d.
Vì C nằm giữa A và B nên AC + CB = AB (1)
Lấy điểm C’ bất kỳ trên d (C’ # C)
Nối AC’, BC’.
Trong ∆ABC’ ta có:
AC’ + BC’ > AB (bất đẳng thức tam giác) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: AC’ + C’B > AC + CB
Vậy C là điểm cần tìm.
Câu 25: Ba thành phố A, B C trên bản đồ là ba đỉnh của một tam giác, trong đó AC = 30km, AB = 70km
a) Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 40km thì thành phố B có nhận được tín hiệu không? Vì sao?
b) Cũng hỏi như trên với máy phát sóng có bán kính hoạt động bằng 100km.
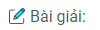
Để giải quyết câu hỏi của bài toán ta cần xét khoảng cách BC.
Trong ∆ABC theo bất đẳng thức của tam giác và hệ quả ta có:
AB – AC < BC < AB + AC
Thay giá trị: AB = 70km, AC = 30km
\( \Rightarrow \) 70 – 30 < BC < 70 + 30 => 40 < BC < 100
a) Nếu máy phát sóng để ở C có bán kính hoạt động bằng 40km thì ở B không nhận được tín hiệu vì BC > 40.
b) Nếu máy phát sóng để ở C có bán kính hoạt động bằng 100km thì ở B nhận được tín hiệu vì BC < 100.
Câu 26: Cho tam giác ABC, điểm D nằm giữa B và C.
Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
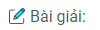
Trong ∆ABD ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ∆ADC ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2):
\(\eqalign{
& 2{\rm{AD}} < AB + B{\rm{D}} + AC + DC \cr
& \Rightarrow 2AD < AB + AC + BC \cr
& \Rightarrow A{\rm{D}} < {{AB + AC + BC} \over 2} \cr} \)

