Câu 89: Cho hình 20 trong đó giao điểm O của hai đường thẳng a và a nằm ngoài phạm vi tờ giấy. Chỉ vẽ hình trong phạm vi tờ giấy, hãy vẽ đường thẳng d đi qua A sao cho đường thẳng d cũng đi qua O nếu kéo dài đường thẳng d ra ngoài phạm vi tờ giấy.
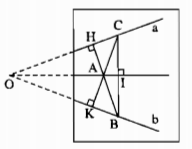
– Kẻ \(AH \bot a\) kéo dài, HA cắt b tại B.
– Kẻ \(AK \bot b\) kéo dài KA cắt a tại C.
– Kẻ \(AI \bot BC\), đường thẳng AI đi qua O.
Vì trong ∆OBC có 2 đường cao BH và CK cắt nhau tại A nên A là trực tâm của ∆OBC.
OA là đường cao thứ 3 nên \(OA \bot BC\)
\(AI \bot BC\) nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.
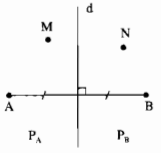
Câu 90: Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là \({P_A}\), phần chứa điểm B ký hiệu là \({P_B}\) (hình dưới)
a) Gọi M là một điểm của \({P_A}\). Chứng minh rằng MA < MB.
b) Gọi N là một điểm của \({P_B}\). Chứng minh rằng NB < NA.
c) Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu trong \({P_A}\),\({P_B}\) hay trên d?
a) Giải tương tự như bài 57, ta có MA < MB.
b) Giải tương tự như câu a, ta có NB < NA
Advertisements (Quảng cáo)
c) Nếu K nằm trong \({P_B}\) thì theo câu b ta có
KB < KA, trái với đề bài.
Nếu K nằm trên d thì KA = KB, trái với đề bài.
Vậy K nằm trong \({P_A}\).
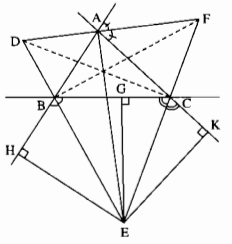
Câu 91: Cho tam giác ABC, các đường phân giác của góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân các đường vuông góc kẻ từ E đến các đường thẳng BC, AB, AC.
a) Có nhận xét gì về các độ dài EH, EG, AK.
b) Chứng minh AE là tia phân giác của góc BAC.
c) Đường phân giác của góc ngoài tại A của tam giác ABC cắt đường thẳng BE, CE tại D, F. Chứng minh rằng AE vuông góc với DF.
d) Các đường thẳng AE, BF, CD là các đường gì trong tam giác ABC?
e) Các đường thẳng AE, FB, DC là các đường gì trong tam giác DEF?
Advertisements (Quảng cáo)
a) E thuộc tia phân giác của \(\widehat {CBH}\)
\( \Rightarrow \) EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của \(\widehat {BCK}\)
\( \Rightarrow \) EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
\( \Rightarrow \) E thuộc tia phân giác của \(\widehat {BAC}\) mà E # A
Vậy AE là tia phân giác của \(\widehat {BAC}\)
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
\( \Rightarrow \) \(A{\rm{E}} \bot {\rm{AF}}\) (tính chất hai góc kề bù)
Hay \(A{\rm{E}} \bot {\rm{DF}}\)
d) Chứng minh tương tự câu a ta có BF là tia phân giác của \(\widehat {ABC}\)
CD là tia phân giác của \(\widehat {ACB}\)
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
\(\Rightarrow BF \bot BE\) (tính chất hai góc kề bù)
Hay \(BF \bot E{\rm{D}}\)
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
\( \Rightarrow C{\rm{D}} \bot CE\) (tính chất hai góc kề bù)
Hay \(C{\rm{D}} \bot {\rm{EF}}\)

