Câu 19: Có thể có tam giác nào mà độ dài ba cạnh như sau không:
a) 5cm; 10cm; 12cm? b) 1m; 2m; 3,3m?
c) 1,2m; 1m; 2,2m?
a) 5 + 10 > 12; 5 + 12 > 10; 10 + 12 > 5
Vậy có tam giác mà ba cạnh của nó là 5cm; 10cm; 12cm.
b) 1 + 2 < 3,3
Không có tam giác mà ba cạnh của nó là 1m; 2m; và 3,3 m vì tổng hai cạnh bé hơn một cạnh.
c) 1,2 + 1 = 2,2
Không có tam giác mà ba cạnh của nó là: 1,2m; 1m; 2,2m vì tổng hai cạnh bằng một cạnh.
Câu 20: Cho tam giác ABC có AB = 4cm; AC = 1cm. Hãy tìm độ dài cạnh BC biết rằng độ dài này là một số nguyên (cm).
Advertisements (Quảng cáo)
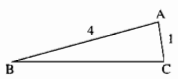
Theo bất đẳng thức tam giác và hệ quả ta có:
AB – AC < BC < AB + AC
\( \Rightarrow \) 4 – 1 < BC < 4 + 1
\( \Rightarrow \) 2 < BC < 5
Vì độ dài cạnh BC là một số nguyên nên BC = 4cm.
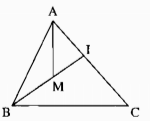
Câu 21: Cho hình dưới. Chứng minh rằng MA + MB < IA + IB < CA + CB
Advertisements (Quảng cáo)
Trong ∆AMI ta có:
MA < MI + IA (bất đẳng thức tam giác)
Cộng vào 2 vế với MB ta có:
MA + MB < MI + IA + MB
\( \Rightarrow \) MA + MB < IB + IA (1)
Trong ∆BIC ta có:
IB < IC + CB (bất đẳng thức tam giác)
Cộng vài 2 vế với IA ta có:
IB + IA < IC + CB + IA
\( \Rightarrow \) IB + IA < CA + CB (2)
Từ (1) và (2) suy ra: MA + MB < IB + IA < CA + CB
Câu 22: Tính chu vi của một tam giác cân có hai cạnh bằng 4m và 9m.
Cạnh 4m không thể là cạnh bên vì nếu cạnh bên là 4m
Ta có: 4 + 4 < 9 trái bất đẳng thức tam giác
Vậy cạnh 4m là cạnh đáy nên cạnh bên là 9m
Ta có chu vi của tam giác đó là 4 + 9 + 9 = 22 m.

