Câu 27: Cho điểm M nằm trong tam giác ABC. Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi tam giác ABC.
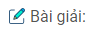
Trong ∆AMB ta có:
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ∆AMC ta có:
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ∆BMC ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế của (1), (2) và (3) ta có:
2(MA + MB + MC) > AB + AC + BC
Suy ra: \(MA + MB + MC > {{AB + AC + BC} \over 2}\)
Câu 28: Tính chu vi của một tam giác cân biết độ dài hai cạnh của nó bằng 3dm và 5dm.
Advertisements (Quảng cáo)
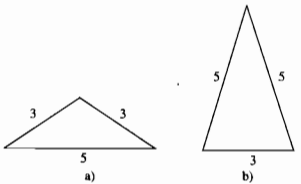
Vì tam giác cân hai cạnh bên bằng nhau. Trong hai số đo 3dm và 5dm có một số đo độ dài cạnh bên và một số đo độ dài cạnh đáy.
Nếu 3dm độ dài cạnh bên ta có: 3 + 3 > 5: tồn tại tam giác
Chu vi tam giác cân là: 3 + 3 + 5 = 11 (dm)
Nếu 5dm độ dài cạnh bên ta có: 5 + 5 > 3: tồn tại tam giác
Chu vi tam giác cân là: 5 + 5 + 3 = 13 (dm).
Câu 29: Độ dài hai cạnh của một tam giác bằng 7cm và 2cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimét là một số tự nhiên lẻ.
Advertisements (Quảng cáo)
Giả sử ∆ ABC có AB = 7cm, AC = 2cm. Theo định lý và hệ quả về quan hệ giữa các cạnh trong một tam giác ta có:
AB – AC < BC < AB + AC => 7 – 2 < BC < 7 + 2 => 5 < BC < 9
Vì số đo cạnh BC là một số tự nhiên lẻ nên BC = 7(cm)
Câu 30
Cho tam giác ABC. Gọi M là trung điểm của BC.
Chứng minh rằng \(AM < {{AB + AC} \over 2}\)
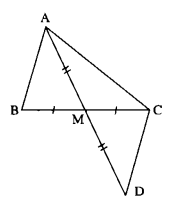
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Xét ∆AMB và ∆DMC:
MA = MD (theo cách vẽ)
\(\widehat {AMB} = \widehat {DMC}\) (đối đỉnh)
MB = MC (gt)
Do đó: ∆AMB = ∆DMC (c.g.c)
\( \Rightarrow \) AB = BC (hai cạnh tương ứng)
Trong ∆ACD ta có:
AD < AC + CD (bất đẳng thức tam giác)
Mà AD = AM + MD = 2AM
CD = AB
\(2{\rm{A}}M < AC + AB \Rightarrow AM < {{AB + AC} \over 2}\)

