Câu 15: Cho tam giác ABC vuông tại A, M là trung điểm của AC. Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM. Chứng minh rằng \(AB < {{BE + BF} \over 2}\)
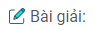
Trong ∆ABM có \(\widehat {BAM} = 90^\circ \)
\( \Rightarrow \) AB < BM
Mà BM = BE + EM = BF – MF
Do đó: AB < BE + EM (1)
AB < BF – FM (2)
Suy ra: AB + AB < BE + ME + BF – MF (3)
Xét hai tam giác vuông AEM và CFM:
\(\widehat {A{\rm{E}}M} = \widehat {CFM} = 90^\circ \)
AM = CM (gt)
\(\widehat {AM{\rm{E}}} = \widehat {CMF}\) (đối đỉnh)
Suy ra: ∆AEM = ∆CFM (cạnh huyền góc nhọn)
Advertisements (Quảng cáo)
\( \Rightarrow \) ME = MF (4)
Từ (3) và (4) suy ra : AB + AB < BE + BF
\( \Rightarrow 2{\rm{A}}B < BE + BF \Rightarrow AB < {{BE + BF} \over 2}\)
Câu 16: Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC.
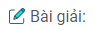
Kẻ \(AH \bot BC\)
a) Nếu H trùng với D: ta có AH < AC (đường vuông góc ngắn hơn đường xiên)
Suy ra: AD < AC
Advertisements (Quảng cáo)
b) Điểm H # D
Giả sử D nằm giữa H và C
Ta có: HD < HC
\( \Rightarrow \) AD < AC (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy AD nhỏ hơn cạnh bên của tam giác cân ABC.
Câu 17: Cho hình sau trong đó AB > AC. Chứng minh rằng EB > AC.
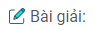
AB > AC (gt)
\( \Rightarrow \) HB > HC (đường xiên lớn hơn có hình chiếu lớn hơn)
Suy ra: EB > EC (hình chiếu lớn hơn có đường xiên lớn hơn)
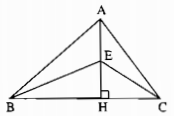
Câu 18: Cho hình sau. Chứng minh rằng: BD + CE < AB + AC.
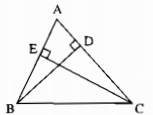
∆ABD có \(\widehat {A{\rm{D}}B} = 90^\circ \)
\( \Rightarrow \) BD < BD (đường vuông góc ngắn hơn đường xiên) (1)
∆AEC có \(\widehat {A{\rm{E}}C} = 90^\circ \)
\( \Rightarrow \) CE < AC (cạnh huyền lớn hơn cạnh góc vuông) (2)
Cộng từng vế (1) và (2)
Suy ra: BD + CE < AB + AC.

