Bài 1.1: Xét sự đồng biến, nghịch biến của các hàm số:
a) \(y = 3{x^2} – 8{x^3}\)
b) \(y = 16x + 2{x^2} – {{16} \over 3}{x^3} – {x^4}\)
c) \(y = {x^3} – 6{x^2} + 9x\)
d) \(y = {x^4} + 8{x^2} + 5\)

a) TXĐ: R
\(y’ = 6x – 24{x^2} = 6x(1 – 4x)\)
y’ = 0 <=> \(\left[ {\matrix{{x = 0} \cr {x = {1 \over 4}} \cr} } \right.\)
y’ > 0 trên khoảng (0;\({1 \over 4}\) ) , suy ra y đồng biến trên khoảng (0;\({1 \over 4}\) )
y’ < 0 trên các khoảng (-∞;0 ); \(({1 \over 4}; + \infty )\), suy ra y nghịch biến trên các khoảng (-∞;0 ); \(({1 \over 4}; + \infty )\)
b) TXĐ: R
\(y’ = 16 + 4x – 16{x^2} – 4{x^3} = – 4(x + 4)({x^2} – 1)\)
y’ = 0 <=> \(\left[ {\matrix{{x = – 4} \cr {x = – 1} \cr {x = 1} \cr} } \right.\)
Bảng biến thiên:
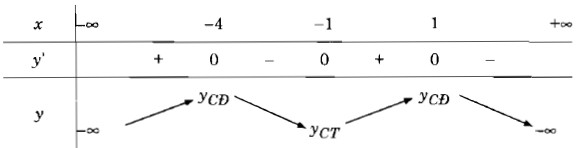
Vậy hàm số y đã cho đồng biến trên các khoảng (-∞; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; +∞)
c) TXĐ: R
\(y’ = 3{x^2} – 12x + 9\)
y’=0 <=> \(\left[ {\matrix{{x = 1} \cr {x = 3} \cr} } \right.\)
y’ > 0 trên các khoảng (-∞; 1), (3; +∞) nên y đồng biến trên các khoảng (-∞; 1), (3; +∞)
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
\(y’ = 4{x^3} + 16 = 4x({x^2} + 4)\)
y’ = 0 <=> x = 0
y’ > 0 trên khoảng (0; +∞) => y đồng biến trên khoảng (0; +∞)
y’ < 0 trên khoảng (-∞; 0) => y nghịch biến trên khoảng (-∞; 0)
Bài 1.2: Tìm các khoảng đồng biến, nghịch biến của các hàm số:
a) \(y = {{3 – 2x} \over {x + 7}}\)
b) \(y = {1 \over {{{(x – 5)}^2}}}\)
c) \(y = {{2x} \over {{x^2} – 9}}\)
d) \(y = {{{x^4} + 48} \over x}\)
e) \(y = {{{x^2} – 2x + 3} \over {x + 1}}\)
Advertisements (Quảng cáo)
g) \(y = {{{x^2} – 5x + 3} \over {x – 2}}\)

a) TXĐ: R\ {-7}
\(y’ = {{ – 17} \over {{{(x + 7)}^2}}}\)
y’ < 0 trên các khoảng (-∞; -7), (-7; +∞) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R\ {5}
\(y’ = {{ – 2} \over {{{(x – 5)}^3}}}\)
y’ < 0 trên khoảng (5; +∞) nên y nghịch biến trên khoảng (5; +∞)
y’ > 0 trên khoảng (-∞; 5) nên y đồng biến trên khoảng (-∞; 5)
c) TXĐ: R\{-3; 3}
\(y’ = {{ – 2({x^2} + 9)} \over {{{({x^2} – 9)}^2}}}\)
y’ < 0 trên các khoảng (-∞; – 3), (-3; 3), (3; +∞) nên hàm số đã cho nghịch biến trên các khoảng đó.
d) TXĐ: R\ {0}
\(y’ = {{3({x^4} – 16)} \over {{x^2}}} = {{3({x^2} – 4)({x^2} + 4)} \over {{x^2}}}\)
y’ = 0 <=> \(\left[ {\matrix{{x = – 2} \cr {x = 2} \cr} } \right.\)
Bảng biến thiên:
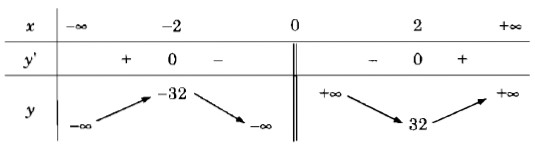
Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)
e) TXĐ: R \ {-1}
\(y’ = {{{x^2} + 2x – 5} \over {{{(x + 1)}^2}}}\)
y’ = 0 <=> \(\left[ {\matrix{{x = – 1 – \sqrt 6 } \cr {x = – 1 + \sqrt 6 } \cr} } \right.\)
Advertisements (Quảng cáo)
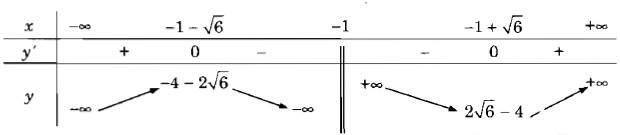
Vậy hàm số đã cho đồng biến trên các khoảng \(( – \infty ; – 1 – \sqrt 6 ),( – 1 + \sqrt 6 ; + \infty )\)
và nghịch biến trên các khoảng \(( – 1 – \sqrt 6 ; – 1),( – 1; – 1 + \sqrt 6 )\)
g) TXĐ: R\ {2}
\(y’ = {{{x^2} – 4x + 7} \over {{{(x – 2)}^2}}} > 0\)
(do \({x^2} – 4x + 7\) có ∆’ = – 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng \(( – \infty ;2),(2; + \infty )\)
Bài 1.3: Xét tính đơn điệu của các hàm số:
a) \(y = \sqrt {25 – {x^2}} \)
b) \(y = {{\sqrt x } \over {x + 100}}\)
c) \(y = {x \over {\sqrt {16 – {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} – 6} }}\)

a) TXĐ: [-5; 5]
\(y’ = {{ – x} \over {\sqrt {25 – {x^2}} }}\) ; y’ = 0 <=> x = 0
Bảng biến thiên:
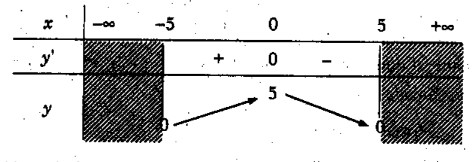
Vậy hàm số đồng biến trên khoảng (-5; 0) nghịch biến trên khoảng (0; 5)
b) TXĐ: [0; +∞)
\(y’ = {{100 – x} \over {2\sqrt x {{(x + 100)}^2}}}\) ; y’ = 0 <=> x = 100
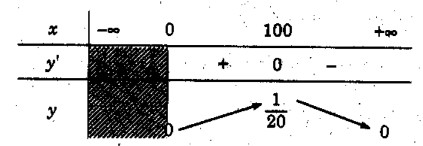
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; +∞)
c) TXĐ: (-4; 4)
\(y’ = {{16} \over {(16 – {x^2})\sqrt {16 – {x^2}} }} > 0\) ; ∀ x ∈ (-4; 4).
Vậy hàm số đồng biến trên khoảng (-4; 4).
d) TXĐ: (-∞; \(\sqrt 6 \)) ∪ (\(\sqrt 6 \); +∞)
\(y’ = {{2{x^2}({x^2} – 9)} \over {({x^2} – 6)\sqrt {{x^2} – 6} }}\) ; y’ = 0 <=> x = ±3
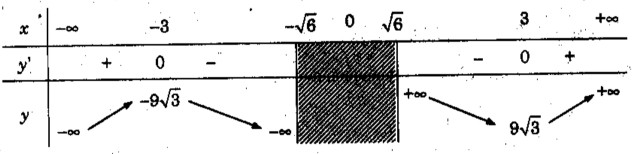
Vậy hàm số đồng biến trên các khoảng (-∞; -3), (3; +∞), nghịch biến trên các khoảng (-3;\(-\sqrt 6 \) ), (\(\sqrt 6 \); 3).
Bài 1.4: Xét sự đồng biến, nghịch biến của các hàm số:
a) \(y = x – {\mathop{\rm s}\nolimits} {\rm{inx}}\), x ∈ [0; 2π].
b) \(y = x + 2\cos x\) , x ∈ \(({\pi \over 6};{{5\pi } \over 6})\)
c) \(y = \sin {1 \over x}\) , (x > 0)

a) \(y = x – {\mathop{\rm s}\nolimits} {\rm{inx}}\), x ∈ [0; 2π].
\(y’ = 1 – c{\rm{osx }}\) ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
b) \(y = x + 2\cos x\) , x ∈ \(({\pi \over 6};{{5\pi } \over 6})\)
\(y’ = 1 – 2\sin x\) < 0 với x ∈ \(({\pi \over 6};{{5\pi } \over 6})\)
Do đó, hàm số nghịch biến trên khoảng \(({\pi \over 6};{{5\pi } \over 6})\)
c) Xét hàm số \(y = \sin {1 \over x}\) với x > 0.
\(y’ = – {1 \over {{x^2}}}\cos {1 \over x}\)
Giải bất phương trình sau trên khoảng (0; +∞):
\({1 \over {{x^2}}}( – \cos {1 \over x}) > 0\) ⟺ \(\cos {1 \over x}\) < 0
⟺ \({\pi \over 2}(1 + 4k) < {1 \over x} < {\pi \over 2}(3 + 4k)\) ,k = 0, 1, 2 ….
⟺ \({2 \over {\pi (1 + 4k)}} > x > {2 \over {\pi (3 + 4k)}}\) , k = 0, 1, 2 ……..
Do đó, hàm số đồng biến trên các khoảng
\(…,({2 \over {(4k + 3)\pi }};{2 \over {(4k + 1)\pi }}),({2 \over {(4k – 1)\pi }};{2 \over {(4k – 3)\pi }}),…,\) \(({2 \over {7\pi }};{2 \over {5\pi }}),({2 \over {3\pi }};{2 \over \pi })\)
Và nghịch biến trên các khoảng
……, \(({2 \over {(4k + 1)\pi }};{2 \over {(4k – 1)\pi }}),({2 \over {5\pi }};{2 \over {3\pi }}),…,({2 \over \pi }; + \infty )\)
với k = 0, 1, 2 …

