Bài 1.11: Tìm cực trị của các hàm số sau:
a) \(y = – 2{x^2} + 7x – 5\)
b) \(y = {x^3} – 3{x^2} – 24x + 7\)
c) \(y = {x^4} – 5{x^2} + 4\)
d) \(y = {(x + 1)^3}(5 – x)\)
e) \(y = {(x + 2)^2}{(x – 3)^3}\)
a) \(y = – 2{x^2} + 7x – 5\) . TXĐ: R
\(\eqalign{
& y’ = – 4x + 7,y’ = 0 < = > x = {7 \over 4} \cr
& y” = – 4 = > y”({7 \over 4}) = – 4 < 0 \cr} \)
Vậy \(x = {7 \over 4}\) là điểm cực đại của hàm số và \({y_{CD}} = {9 \over 8}\)
b) \(y = {x^3} – 3{x^2} – 24x + 7\) . TXĐ: R
\(y’ = 3{x^2} – 6x – 24 = 3({x^2} – 2x – 8)\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = – 2 \hfill \cr
x = 4 \hfill \cr} \right.\)
Vì \(y”( – 2) = – 18 < 0,y”(4) = 18 > 0\) nên hàm số đạt cực đại tại x = – 2 ; đạt cực tiểu tại x = 4 và yCĐ = y(-2) = 35 ; yCT = y(4) = -73.
c) \(y = {x^4} – 5{x^2} + 4\)
TXĐ: R
\(\eqalign{
& = {{2{x^2} – 2{m^2} – {x^2} – 2mx + 3} \over {{{(x – m)}^2}}} = {{{x^2} – 2mx – 2{m^2} + 3} \over {{{(x – m)}^2}}} \cr
& y’ = 4{x^3} – 10x = 2x(2{x^2} – 5) \cr} \)
$$y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = – \sqrt {{5 \over 2}} \hfill \cr
x = \sqrt {{5 \over 2}} \hfill \cr} \right.$$
Vì \(y”( \pm \sqrt {{5 \over 2}} ) = 20 > 0,y”(0) = – 10 < 0\)
Nên hàm số đạt cực đại tại x = 0, đạt cực tiểu tại \(x = \pm \sqrt {{5 \over 2}} \) và ta có:
yCĐ = y(0) = 4 , \({y_{_{CT}}} = y( \pm \sqrt {{5 \over 2}} ) = – {9 \over 4}\)
d) TXĐ: R
\(y’ = – {(x + 1)^3} + 3{(x + 1)^2}(5 – x) = 2{(x + 1)^2}(7 – 2x)\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = – 1 \hfill \cr
x = {7 \over 2} \hfill \cr} \right.\)
Bảng biến thiên:
Hàm số đạt cực đại tại \(x = {7 \over 2};{y_{CD}} = y({7 \over 2}) = {{2187} \over {16}}\)
e) TXĐ: R
\(y’ = 2(x + 2){(x – 3)^3} + 3{(x + 2)^2}{(x – 3)^2} = 5x(x + 2){(x – 3)^2}\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = – 2 \hfill \cr
x = 0 \hfill \cr
x = 3 \hfill \cr} \right.\)
Bảng biến thiên:
Từ đó suy ra yCĐ = y(-2) = 0 ; yCT = y(0) = -108.
Bài 1.12: Tìm cực trị của các hàm số sau:
a) \(y = {{x + 1} \over {{x^2} + 8}}\)
b) \(y = {{{x^2} – 2x + 3} \over {x – 1}}\)
Advertisements (Quảng cáo)
c) \(y = {{{x^2} + x – 5} \over {x + 1}}\)
d) \(y = {{{{(x – 4)}^2}} \over {{x^2} – 2x + 5}}\)
a) TXĐ : R
\(y’ = {{{x^2} + 8 – 2x(x + 1)} \over {{{({x^2} + 8)}^2}}} = {{ – {x^2} – 2x + 8} \over {{{({x^2} + 8)}^2}}}\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = – 4 \hfill \cr
x = 2 \hfill \cr} \right.\)
Bảng biến thiên:
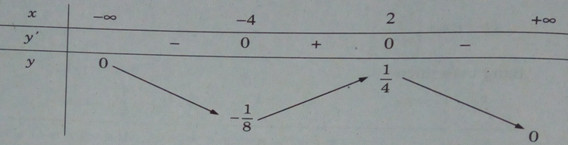Hàm số đạt cực đại tại x = 2, cực tiểu tại x = – 4 và \({y_{CD}} = y(2) = {1 \over 4};{y_{CT}} = y( – 4) = – {1 \over 8}\)
b) Hàm số xác định và có đạo hàm với mọi x ≠ 1.
\(y’ = {{{x^2} – 2x – 1} \over {{{(x – 1)}^2}}}\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = 1 – \sqrt 2 \hfill \cr
x = 1 + \sqrt 2 \hfill \cr} \right.\)
Bảng biến thiên:
Hàm số đạt cực đại tại \(x = 1 – \sqrt 2 \) và đạt cực tiểu tại \(x = 1 + \sqrt 2\) , ta có:
\({y_{CD}} = y(1 – \sqrt 2 ) = – 2\sqrt 2 ;{y_{CT}} = y(1 + \sqrt 2 ) = 2\sqrt 2 \)
c) TXĐ: R\{-1}
\(y’ = {{{x^2} + 2x + 6} \over {{{(x + 1)}^2}}} > 0,\forall x \ne – 1\)
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
d) \(y = {{{{(x – 4)}^2}} \over {{x^2} – 2x + 5}}\)
Vì x2 – 2x + 5 luôn luôn dương nên hàm số xác định trên \(( – \infty ; + \infty )\)
\(y’ = {{2(x – 4)({x^2} – 2x + 5) – {{(x – 4)}^2}(2x – 2)} \over {{{({x^2} – 2x + 5)}^2}}} = {{2(x – 4)(3x + 1)} \over {{{({x^2} – 2x + 5)}^2}}}\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = – {1 \over 3} \hfill \cr
x = 4 \hfill \cr} \right.\)
Bảng biến thiên:
Advertisements (Quảng cáo)
Hàm số đạt cực đại tại \(x = – {1 \over 3}\) , đạt cực tiểu tại x = 4 và \({y_{CD}} = y( – {1 \over 3}) = {{13} \over 4};{y_{CT}} = y(4) = 0\)
Bài 1.13: Tìm cực trị của các hàm số sau:
a) \(y = x – 6\root 3 \of {{x^2}} \)
b) \(y = (7 – x)\root 3 \of {x + 5}\)
c) \(y = {x \over {\sqrt {10 – {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} – 6} }}\)
a) TXĐ: R
\(y’ = 1 – {4 \over {\root 3 \of x }} = {{\root 3 \of x – 4} \over {\root 3 \of x }}\)
\(y’ = 0 < = > x = 64\)
Bảng biến thiên:
Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
b) Hàm số xác định trên khoảng \(( – \infty ; + \infty )\) .
\(y’ = – \root 3 \of {x + 5} + {{7 – x} \over {3\root 3 \of {{{(x + 5)}^2}} }} = {{ – 4(x + 2)} \over {3\root 3 \of {{{(x + 5)}^2}} }}\)
Bảng biến thiên:
Vậy \({y_{CD}} = y( – 2) = 9\root 3 \of 3 \)
c) Hàm số xác định trên khoảng \(( – \sqrt {10} ;\sqrt {10} )\) .
\(y’ = {{\sqrt {10 – {x^2}} + {{{x^2}} \over {\sqrt {10 – {x^2}} }}} \over {10 – {x^2}}} = {{10} \over {(10 – {x^2})\sqrt {10 – {x^2}} }}\)
Vì y’ > 0 với mọi \(( – \sqrt {10} ;\sqrt {10} )\) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
d) TXĐ: \(D = ( – \infty ; – \sqrt 6 ) \cup (\sqrt 6 ; + \infty )\)
\(\eqalign{
& y’ = {{3{x^2}\sqrt {{x^2} – 6} – {{{x^4}} \over {\sqrt {{x^2} – 6} }}} \over {{x^2} – 6}} \cr
& = {{3{x^2}({x^2} – 6) – {x^4}} \over {\sqrt {{{({x^2} – 6)}^3}} }} \cr
& = {{2{x^2}({x^2} – 9)} \over {\sqrt {{{({x^2} – 6)}^3}} }} \cr} \)
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x =- 3 và \({y_{CT}} = y(3) = 9\sqrt 3 ;{y_{CD}} = y( – 3) = – 9\sqrt 3 \)
Bài 1.14: Tìm cực trị của các hàm số sau:
a) \(y = \sin 2x\)
b) \(y = \cos x – \sin x\)
c) \(y = {\sin ^2}x\)
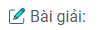
a) \(y = \sin 2x\)
Hàm số có chu kỳ \(T = \pi \)
Xét hàm số \(y = \sin 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) , ta có:
\(y’ = 2\cos 2x\)
\(y = 0 \Leftrightarrow \left[ \matrix{
x = {\pi \over 4} \hfill \cr
x = {{3\pi } \over 4} \hfill \cr} \right.\)
Bảng biến thiên:
Do đó trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) , hàm số đạt cực đại tại \({\pi \over 4}\) , đạt cực tiểu tại \({{3\pi } \over 4}\) và \({y_{CD}} = y({\pi \over 4}) = 1;\,\,{y_{CT}} = y({{3\pi } \over 4}) = – 1\)
Vậy trên R ta có:
\({y_{CĐ}} = y({\pi \over 4} + k\pi ) = 1;\)
\({y_{CT}} = y({{3\pi } \over 4} + k\pi ) = – 1,k \in Z\)
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn \({\rm{[}} – \pi ;\pi {\rm{]}}\).
\(\eqalign{
& y’ = – \sin x – \cos x \cr
& y’ = 0 < => \tan x = – 1 < = > x = – {\pi \over 4} + k\pi ,k \in Z \cr} \)
Lập bảng biến thiên trên đoạn \({\rm{[}} – \pi ;\pi {\rm{]}}\)
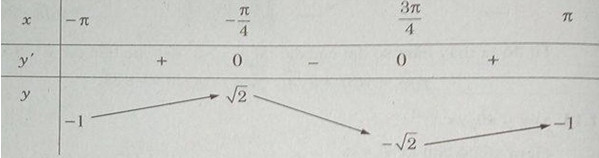
Hàm số đạt cực đại tại \(x = – {\pi \over 4} + k2\pi \) , đạt cực tiểu tại \(x = {{3\pi } \over 4} + k2\pi (k \in Z)\) và
\({y_{CĐ}} = y( – {\pi \over 4} + k2\pi ) = \sqrt 2\) ;
\({y_{CT}} = y({{3\pi } \over 4} + k2\pi ) = – \sqrt 2 (k \in Z)\)
c) Ta có: \(y = {\sin ^2}x = {{1 – \cos 2x} \over 2}\)
Do đó, hàm số đã cho tuần hoàn với chu kỳ \(\pi \). Ta xét hàm số \(y = {1 \over 2} – {1 \over 2}\cos 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) .
\(\eqalign{
& y’ = \sin 2x \cr
& y’ = 0 < = > \sin 2x = 0 < = > x = k.{\pi \over 2}(k \in Z) \cr} \)
Lập bảng biến thiên trên đoạn \(\left[ {0,\pi } \right]\)
Từ đó, ta thấy hàm số đạt cực tiểu tại \(x = k.{\pi \over 2}\) với k chẵn, đạt cực đại tại \(x = k.{\pi \over 2}\) với k lẻ, và
\({y_{CT}} = y(2m\pi ) = 0;\)
\({y_{CĐ}} = y((2m + 1){\pi \over 2}) = 1(m \in Z)\)
