Bài 1.26: Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.
Gọi một trong hai số phải tìm là x, ta có số kia là x + 13
Xét tích:
\(\eqalign{
& p(x) = x(x + 13) = {x^2} + 13x \cr
& p'(x) = 2x + 13;p'(x) = 0 < = > x = – {{13} \over 2} \cr} \)
Bảng biến thiên:
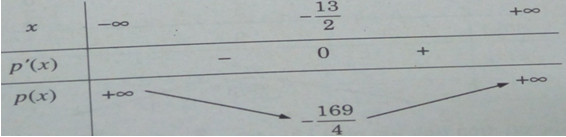
Vậy tích hai số bé nhất khi một số là \( – {{13} \over 2}\) và số kia là \({{13} \over 2}\).
Bài 1.27: Một chất điểm chuyển động theo quy luật s = 6t2 – t3 . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.
Advertisements (Quảng cáo)
 \(s = 6{t^2} – {t^3},t > 0\)
\(s = 6{t^2} – {t^3},t > 0\)
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3t2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng \((2; + \infty )\) .
Advertisements (Quảng cáo)
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó \(\mathop {\max }\limits_{(0; + \infty )} V = {V_{CD}} = v(2) = 12(m/s)\).
Bài 1.28: Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0).
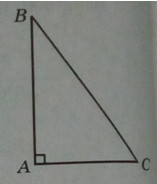
Kí hiệu cạnh góc vuông AB là x, \(0 < x < {a \over 2}\)
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
\(AC = \sqrt {B{C^2} – A{B^2}} = \sqrt {{{(a – x)}^2} – {x^2}} \)
Hay \(AC = \sqrt {{a^2} – 2ax} \)
Diện tích tam giác ABC là:
\(\eqalign{
& S(x) = {1 \over 2}x\sqrt {{a^2} – 2ax} \cr
& S'(x) = {1 \over 2}\sqrt {{a^2} – 2ax} – {1 \over 2}{{ax} \over {\sqrt {{a^2} – 2ax} }} = {{a(a – 3x)} \over {2\sqrt {{a^2} – 2ax} }} \cr
& S'(x) = 0 < = > x = {a \over 3} \cr} \)
Bảng biến thiên:

Tam giác có diện tích lớn nhất khi \(AB = {a \over 3};BC = {{2a} \over 3}\)

