Bài 1.49: Cho hàm số: y = 4x3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
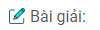
a) \(y = 4{x^3} + x,y’ = 12{x^2} + 1 > 0,\forall x \in R\)
Bảng biến thiên:
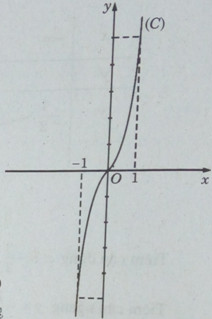
Đồ thị:
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì \(f'({x_0}) = 12x_0^2 + 1 = 13\) (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: \({x_0} = \pm 1\)
Vậy có hai tiếp tuyến phải tìm là \(y = 13x \pm 8\)
c) Vì y’ = 12x2 + m nên : \(m \ge 0:y” = – 6({m^2} + 5m)x + 12m\)
+) Với \(m \ge 0\) ta có y’ > 0 (khi m = 0 ; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi \(m \ge 0:y” = – 6({m^2} + 5m)x + 12m\)
+) Với m < 0 thì \(y{\rm{ }} = {\rm{ }}0 \Leftrightarrow x = \pm \sqrt {{{ – m} \over {12}}} \)
Từ đó suy ra:
y’ > 0 với \( – \infty < x < – \sqrt {{{ – m} \over {12}}} \) và \(\sqrt {{{ – m} \over {12}}} < x < + \infty \)
y’ < 0 với \( – \sqrt {{{ – m} \over {12}}} < x < \sqrt {{{ – m} \over {12}}} \)
Vậy hàm số (1) đồng biến trên các khoảng \(( – \infty ; – \sqrt {{{ – m} \over {12}}} ),(\sqrt {{{ – m} \over {12}}} ; + \infty )\) và nghịch biến trên khoảng \(( – \sqrt {{{ – m} \over {12}}} ;\sqrt {{{ – m} \over {12}}} )\)
Bài 1.50: Cho hàm số: y = x3 + mx2 – 3 (1)
a) Xác định m để hàm số (1) luôn luôn có cực đại, cực tiểu.
b) Chứng minh rằng phương trình: x3 + mx2 – 3 = 0 (2) luôn luôn có một nghiệm dương với mọi giá trị m thuộc R.
c) Xác định m để phương trình (2) có một nghiệm duy nhất.
Hàm số \(y = {x^3} + m{x^2} – 3\) xác định và có đạo hàm trên R.
\(y’ = 3{x^2} + 2mx = x(3x + 2m)\)
Advertisements (Quảng cáo)
Để hàm số có cực đại , cực tiểu thì phương trình y’ = 0 phải có hai nghiệm phân biệt:
\({x_1} = 0;{x_2} = {{ – 2m} \over 3} \ne 0\)
Muốn vậy phải có \(m \ne 0\)
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } ({x^3} + m{x^2} – 3) = + \infty \) và \(y(0) = -3 < 0.\)
Vậy với mọi m, phương trình x3 + mx2 – 3 = 0 luôn luôn có nghiệm dương.
c) Phương trình f(x) = x3 + mx2 – 3 = 0 có duy nhất một nghiệm khi và chỉ khi cực đại và cực tiểu của hàm số y = f(x) cùng dấu, tức là:
\(\eqalign{
& f(0)f( – {{2m} \over 3}) > 0 \cr
& \Leftrightarrow ( – 3)( – {{8{m^3}} \over {27}} + {{4{m^3}} \over 9} – 3) > 0 \cr&\Leftrightarrow 8{m^3} – 12{m^3} + 81 > 0 \cr
& \Leftrightarrow 4{m^3} < 81 \Leftrightarrow m < 3\root 3 \of {{3 \over 4}} (m \ne 0) \cr} \)
Bài 1.51: Cho hàm số: \(y = – ({m^2} + 5m){x^3} + 6m{x^2} + 6x – 5\)
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
a) \(\eqalign{
& y = – ({m^2} + 5m){x^3} + 6m{x^2} + 6x – 5 \cr
& y’ = – 3({m^2} + 5m){x^2} + 12mx + 6 \cr} \)
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) \({m^2} + 5m = 0 \Leftrightarrow \left[ \matrix{
m = 0 \hfill \cr
m = – 5 \hfill \cr} \right.\)
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
Advertisements (Quảng cáo)
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với \({m^2} + 5m \ne 0\) Khi đó, y’ không đổi dấu nếu
\(\eqalign{
& \Delta ‘ = 36{m^2} + 18({m^2} + 5m) \le 0 \cr
& \Leftrightarrow 3{m^2} + 5m \le 0 \Leftrightarrow – {5 \over 3} \le m \le 0 \cr} \)
– Với điều kiện đó, ta có \( – 3({m^2} + 5m) > 0\) nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện \( – {5 \over 3} \le m \le 0\) thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
\(y'(1) = – 3{m^2} – 3m + 6 = 0 \Leftrightarrow \left[ \matrix{
m = 1 \hfill \cr
m = – 2 \hfill \cr} \right.\)
Mặt khác, \(y” = – 6({m^2} + 5m)x + 12m\)
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
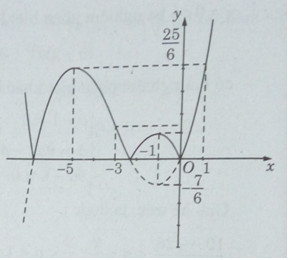
Bài 1.52: Cho hàm số \(y = {{(a – 1){x^3}} \over 3} + a{x^2} + (3a – 2)x\)
a) Xác định a để hàm số luôn luôn đồng biến.
b) Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với \(a = {3 \over 2}\).
Từ đó suy ra đồ thị của hàm số: \(y = |{{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2}|\)
a) Ta có:
\(\eqalign{
& y’ = 15{x^4} + 5 > 0,\forall x \in R \cr
& y = {{(a – 1){x^3}} \over 3} + a{x^2} + (3a – 2)x \cr
& y’ = (a – 1){x^2} + 2ax + 3a – 2 \cr} \) .
+)Với a = 1, y’ = 2x + 1 đổi dấu khi x đi qua \( – {1 \over 2}\) . Hàm số không luôn luôn đồng biến.
+) Với \(a \ne 1\) thì với mọi x mà tại đó \(y’ \ge 0\)
\(\Leftrightarrow \left\{ \matrix{
a – 1 > 0 \hfill \cr
\Delta ‘ = – 2{a^2} + 5a – 2 \le 0 \hfill \cr} \right. \Leftrightarrow a \ge 2\)
(y’ = 0 chỉ tại x = -2 khi a = 2)
Vậy với \(a \ge 2\) hàm số luôn luôn đồng biến.
b) Đồ thị cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình y = 0 có ba nghiệm phân biệt. Ta có:
\(\eqalign{
& y = 0 \Leftrightarrow x{\rm{[}}{{(a – 1){x^2}} \over 3} + ax + 3a – 2] = 0 \cr
& \Leftrightarrow x{\rm{[}}(a – 1){x^2} + 3ax + 9a – 6] = 0 \cr} \)
y = 0 có ba nghiệm phân biệt khi và chỉ khi phương trình:
\((a – 1){x^2} + 3ax + 9a – 6 = 0\) có hai nghiệm phân biệt khác 0.
Muốn vậy, ta phải có:
\(\left\{ \matrix{
a – 1 \ne 0 \hfill \cr
\Delta = 9{a^2} – 4(a – 1)(9a – 6) > 0 \hfill \cr
9a – 6 \ne 0 \hfill \cr} \right.\)
Giải hệ trên ta được:
\({{10 – \sqrt {28} } \over 9} < a < {2 \over 3};{2 \over 3} < a < 1;1 < a < {{10 + \sqrt {28} } \over 9}\)
c) Khi \(a = {3 \over 2}\) thì \(y = {{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2}\)
\(y’ = {{{x^2}} \over 2} + 3x + {5 \over 2}\)
\(y’ = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \matrix{
x = – 1 \hfill \cr
x = – 5 \hfill \cr} \right.\)
Bảng biến thiên:
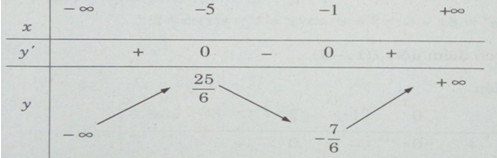Đồ thị
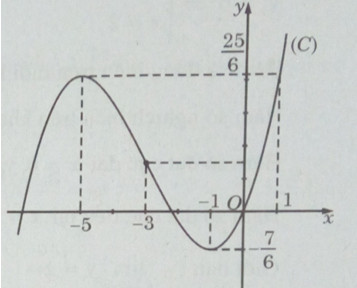Vì \(|{{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2}| = \left\{ \matrix{
{{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2},{{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2} \ge 0 \hfill \cr
– ({{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2}),{{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2} < 0 \hfill \cr} \right.\)
Nên từ đồ thị (C) ta suy ra ngay đồ thị hàm số: \(y = |{{{x^3}} \over 6} + {{3{x^2}} \over 2} + {{5x} \over 2}|\)
