Bài ôn tập chương III phần hình học Sách bài tập Toán Hình học 10. Giải bài 3.40, 3.41, 3.42 trang 161 Sách bài tập Toán Hình học 10. Câu 3.40: Trong mặt phẳng Oxy cho đường thẳng…
Bài 3.40: Trong mặt phẳng Oxy cho đường thẳng \(\Delta 😡 – y + 2 = 0\) và điểm A(2;0).
a) Chứng mình rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng .
b) Tìm điểm M trên \(\Delta \) sao cho độ dài đường gấp khúc OMA ngắn nhất.

(h.3.11)
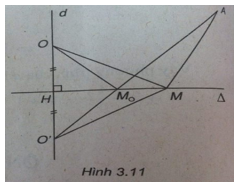
Ta có:
\(\Delta \left( O \right) = 2 > 0\)
\(\Delta \left( A \right) = 2 + 2 > 0\)
Vậy A và O nằm về cùng một phía đối với \(\Delta \)
b) Gọi O’ là điểm đối xứng của O qua \(\Delta \), ta có:
\(OM + MA = O’M + MA \ge O’A\)
Advertisements (Quảng cáo)
Ta có : OM + MA ngắn nhất
\( \Leftrightarrow O’,M,A\) thẳng hàng
Xét đường thẳng d đi qua O và vuông góc với \(\Delta \) . Phương trình của d là:
x + y = 0
d cắt \(\Delta \) tại H(-1;1).
H là trung điểm của OO’ suy ra \(O’\left( { – 2;2} \right)\)
Phương trình đường thẳng O’A là: x + 2y – 2 = 0
Giải hệ phương trình
Advertisements (Quảng cáo)
\(\left\{ \matrix{
x + 2y = 2 \hfill \cr
x – y = – 2 \hfill \cr} \right.\)
ta được \(M = \left( { – {2 \over 3};{4 \over 3}} \right).\)
Bài 3.41: Cho ba điểm A(3;5), B(2;3), C(6;2).
a) Viết phương trình đường tròn (C) ngoại tiếp tam giác ABC.
b) Hãy xác định tọa độ của tâm và bán kính của (C).

a) (C) : \({x^2} + {y^2} – {{25} \over 3}x – {{19} \over 3}y + {{68} \over 3} = 0.\)
b) (C) có tâm \(I\left( {{{25} \over 6};{9 \over 6}} \right)\) và bán kính \(R = \sqrt {{{85} \over {18}}} .\)
Bài 3.42: Cho phương trình \({x^2} + {y^2} – 2mx – 4(m – 2)y + 6 – m = 0\,(1)\)
a) Tìm điều kiện của m để (1) là phương tình của đường tròn, ta kí hiệu là (C m).
b) Tìm tập hợp các tâm của (C m) khi m thay đổi.

a) (1) là phương trình của đường tròn khi và chỉ khi:
\(\eqalign{
& {a^2} + {b^2} – c > 0 \cr
& \Leftrightarrow {m^2} + 4{(m – 2)^2} – 6 + m > 0 \cr} \)
\( \Leftrightarrow 5m – 15m + 10 > 0 \Leftrightarrow \left[ \matrix{
m < 1 \hfill \cr
m > 2. \hfill \cr} \right.\)
b) (C m) có tâm I(x;y) thỏa mãn:
\(\left\{ \matrix{
x = m \hfill \cr
y = 2(m – 2) \hfill \cr} \right. \Leftrightarrow y = 2x – 4.\)
Vậy tập hợp các tâm của (C m) là một phần của đường thẳng \(\Delta :y = 2x – 4\) thỏa mãn điều kiện giới hạn : x2.

