Bài 1.69: Xét xem ba điểm sau có thẳng hàng không?
a) A(2; – 3), B(5;1) và C(8; 5);
b) M(1;2), N(3; 6) và P(4;5).

a) Ta có \(\overrightarrow {AB} = (3;4),\overrightarrow {AC} = (6;8),\overrightarrow {AC} = 2\overrightarrow {AB} \)
=>A, B, C thẳng hàng.
b) \(\overrightarrow {MN} = (2;4);\overrightarrow {MP} = (3;3)\) mà \({2 \over 3} \ne {4 \over 3}\)
Vậy M, N, P không thẳng hàng.
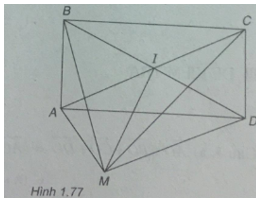
Bài 1.70: Cho hình chữ nhật ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.
a) Với điểm M tùy ý, hãy chứng minh:
\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
b) Chứng minh rằng: \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right|\)

(Xem hình 1.77)
Advertisements (Quảng cáo)
a) \(\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MI} \)
\(\overrightarrow {MB} + \overrightarrow {MD} = 2\overrightarrow {MI}\)
Vậy \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
b) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} = > \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = AC\)
\(\overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {DB} = > \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = DB\)
Vì hai đường chéo của hình chữ nhật dài bằng nhau nên
\(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right|\)
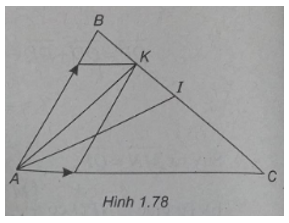
Bài 1.71: Cho tam giác ABC. Gọi I là trung điểm của BC, K là trung điểm của BI.
Advertisements (Quảng cáo)
Chứng minh rằng:
a) \(\overrightarrow {AK} = {1 \over 2}\overrightarrow {AB} + {1 \over 2}\overrightarrow {AI} \)
b) \(\overrightarrow {AK} = {3 \over 4}\overrightarrow {AB} + {1 \over 4}\overrightarrow {AC} \)

(Xem hình 1.78)
a) Vì K là trung điểm của BI nên \(\overrightarrow {AK} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AI} )\) (1)
b) Vì I là trung điểm của BC nên \(\overrightarrow {AI} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} )\) (2)
Thay (2) vào (1) ta được:
\(\overrightarrow {AK} = {1 \over 2}{\rm{[}}\overrightarrow {AB} + {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} ){\rm{]}}\)
\(\overrightarrow {AK} = {3 \over 4}\overrightarrow {AB} + {1 \over 4}\overrightarrow {AC} \)
Bài 1.72: Trong mặt phẳng Oxy cho tam giác đều OAB có cạnh bằng 2, AB song song với Ox, điểm A có hoành độ và tung độ dương.
a) Tìm tọa độ hai đỉnh A và B;
b) Tìm tọa độ trọng tâm G của tam giác OAB.

(Xem hình 1.79)
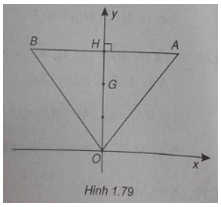
a) Gọi H là trung điểm của AB ta có:
\(OH = {{OA\sqrt 3 } \over 2} = \sqrt 3 ;HA = {{OA} \over 2} = 1\)
Vậy ta có \(A(1;\sqrt 3 )\) và \(B( – 1;\sqrt 3 )\)
b) \(OG = {2 \over 3}OH = {2 \over 3}\sqrt 3 \)
Vậy ta có \(G\left( {0;{{2\sqrt 3 } \over 3}} \right)\)

