Bài 1.65: Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Gọi G và G’ lần lượt là trọng tâm các tam giác MPR và NQS. Ta có:
\(\eqalign{
& \overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} \cr
& = {1 \over 2}(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} + \overrightarrow {GE} + \overrightarrow {GF} ) \cr
& = \overrightarrow 0 \cr} \)
\(\eqalign{
& \overrightarrow {G’N} + \overrightarrow {G’Q} + \overrightarrow {G’S} \cr
& = {1 \over 2}(\overrightarrow {G’B} + \overrightarrow {G’C} + \overrightarrow {G’D} + \overrightarrow {G’E} + \overrightarrow {G’F} + \overrightarrow {G’A} ) \cr
& = \overrightarrow 0 \cr} \)
Do đó:
\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} + \overrightarrow {GE} + \overrightarrow {GF} \cr
& = \overrightarrow {G’B} + \overrightarrow {G’C} + \overrightarrow {G’D} + \overrightarrow {G’E} + \overrightarrow {G’F} + \overrightarrow {G’A} \cr} \)
\( = > 6\overrightarrow {GG’} = \overrightarrow 0 = > G \equiv G’\)
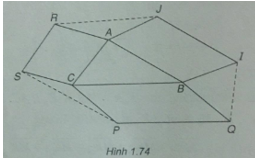
Bài 1.66: Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng:
\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 \)

(Xem hình 1.74)
Advertisements (Quảng cáo)
\(\eqalign{
& \overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} \cr
& = \overrightarrow {RA} + \overrightarrow {AJ} + \overrightarrow {IB} + \overrightarrow {BQ} + \overrightarrow {PC} + \overrightarrow {CS} \cr} \)
\(= (\overrightarrow {RA} + \overrightarrow {CS} ) + (\overrightarrow {AJ} + \overrightarrow {IB} ) + (\overrightarrow {BQ} + \overrightarrow {PC} )\)
\(= \overrightarrow 0 \)
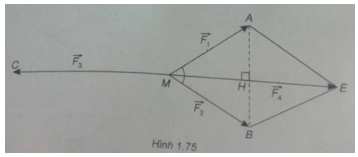
Bài 1.67: Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_12}}\) đều là 100 N và \(\widehat {AMB} = {60^0}\)
a) Đặt \(\overrightarrow {ME} = \overrightarrow {MA} + \overrightarrow {MB} \). Tính độ dài của đoạn ME
b) Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} \)

(Xem hình 1.75)
Advertisements (Quảng cáo)
a) Vật đứng yên là do \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Vẽ hình thoi MAEB ta có: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {ME} \)
Tam giác MAB là tam giác đều có đường cao \(MH = {{100\sqrt 3 } \over 2}\)
Suy ra \(ME = 100\sqrt 3 \)
b) Lực \(\overrightarrow {{F_4}} = \overrightarrow {ME}\) có cường độ là \(100\sqrt 3 N\)
Ta có \(\overrightarrow {{F_4}} + \overrightarrow {{F_3}} = \overrightarrow 0 \), do đó \(\overrightarrow {{F_3}} \) là vec tơ đối của \(\overrightarrow {{F_4}} \). Như vậy \(\overrightarrow {{F_3}} \) có cường độ là \(100\sqrt 3 N\) và ngược hướng với vec tơ \(\overrightarrow {ME} \)
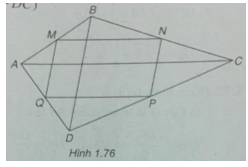
Bài 1.68: Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh rằng:
a) \(\overrightarrow {MN} = \overrightarrow {QP}\)
b) \(\overrightarrow {MP} = \overrightarrow {MN} + \overrightarrow {MQ} \)

(Xem hình 1.76)
a) Ta có:
\(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {BC} ) = {1 \over 2}\overrightarrow {AC} \)
\(\overrightarrow {QP} = \overrightarrow {QD} + \overrightarrow {DP} = {1 \over 2}(\overrightarrow {AD} + \overrightarrow {DC} ) = {1 \over 2}\overrightarrow {AC} \)
Suy ra \(\overrightarrow {MN} = \overrightarrow {QP}\)
b) Tứ giác MNPQ có: \(\left\{ \matrix{
MN{\rm{//}}QD \hfill \cr
MN = QP \hfill \cr} \right.\)
Suy ra MNPQ là hình bình hành.
Suy ra \(\overrightarrow {MP} = \overrightarrow {MN} + \overrightarrow {MQ} \)

