Bài 42: a) \({y^2} = – 2x\) là phương trình chính tắc của parabol.
b) \(y = {x^2}\) là phương trình chính tắc của parabol.
c) Parabol \((P):{y^2} = 2x\) có tiêu điểm F(5, 0) và có đường chuẩn \(\Delta 😡 + 0,5 = 0.\)
d) Parabol \({y^2} = 2px(p > 0)\) có tiêu điểm F(p, 0) và có đường chuẩn \(\Delta 😡 + p = 0.\)
Mệnh đề đúng: c)
Các mệnh đề sai: a), b), d).
Bài 43: Viết phương trình chính tắc của parabol (P) trong mỗi trường hợp sau
a) (P) có tiêu điểm F(3, 0)
Advertisements (Quảng cáo)
b) (P) đi qua điểm M(1, -1)
c) (P) có tham số tiêu là \(p = {1 \over 3}.\)
a) Ta có: \({p \over 2} = 3 \Rightarrow p = 6\)
Advertisements (Quảng cáo)
Phương trình chính tắc của (P) là: \({y^2} = 12x.\)
b) Giả sử \((P):{y^2} = 2px\,(p > 0)\)
\(M\left( {1; – 1} \right) \in \left( P \right)\) nên \({\left( { – 1} \right)^2} = 2p .1 \Rightarrow p = {1 \over 2}\)
Vậy \(\left( P \right):{y^2} = x.\)
c) Phương trình \(\left( P \right):{y^2} = {2 \over 3}x.\)
Bài 44: Cho parabol \({y^2} = 2px.\) Tìm độ dài dây cung của parabol vuông góc với trục đối xứng tại tiêu điểm của parabol (dây cung của parabol là đoạn thẳng nối hai điểm của parabol).
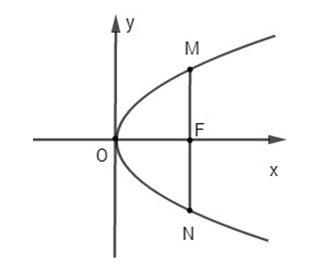
Ta có: \(F\left( {{p \over 2};0} \right)\)
Gọi M là điểm thuộc (P) có hoành độ \(x = {p \over 2}\) thay \(x = {p \over 2}\) vào phương trình của (P) ta được:
\({y^2} = 2p.{p \over 2} = {p^2} \Rightarrow y = \pm p\)
Vậy \(M\left( {{p \over 2};p} \right)\) và \(N\left( {{p \over 2}; – p} \right) \Rightarrow MN = 2p.\)

