Bài 45: Cho dây cung AB đi qua tiêu điểm của parabol (P). Chứng minh rằng khoảng cách từ trung điểm I của dây AB đến đường chuẩn của (P) bằng \({1 \over 2}AB\) . Từ đó có nhận xét gì về đường tròn đường kính AB?
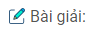
Gọi \(A’,B’,I’\) lần lượt là hình chiếu vuông góc của A,B,I lên đường chuẩn \(\Delta \)
Theo định nghĩa parabol ta có:
Advertisements (Quảng cáo)
\(AA’ = AF\) và \(BB’ = BF\)
\(\eqalign{
& \Rightarrow AB = AF+ FB = AA’ + BB’ = 2II’ \cr
& \Rightarrow II’ = d\left( {I,\Delta } \right) = {{AB} \over 2}. \cr} \)
Từ đó suy ra đường tròn đường kính AB tiếp xúc với đường chuẩn.
Advertisements (Quảng cáo)
Bài 46: Trong mặt phằng tọa độ Oxy cho điểm F(1, -2). Tìm hệ thức giữa x,y để điểm M (x, y) cách đều điểm F và trục hoành.
Phương trình đường thẳng Ox là: \(y=0\)
Ta có: \(MF = d\left( {M,Ox} \right) \Leftrightarrow \sqrt {{{\left( {x – 1} \right)}^2} + {{\left( {y + 2} \right)}^2}} = |y|\)
\( \Leftrightarrow {x^2} – 2x + 1 + {y^2} + 4y + 4 = {y^2}\)
\(\Leftrightarrow y = – {1 \over 4}{x^2} + {1 \over 2}x – {5 \over 4}.\)

