Bài 49: Xét dấu các tam thức bậc hai sau:
a) 3x2 – 2x + 1
b) -x2 + 4x – 1
c) \({x^2} – \sqrt 3 x + {3 \over 4}\)
d) \((1 – \sqrt 2 ){x^2} – 2x + 1 + \sqrt 2 \)
a) Ta có:
a = 3 > 0
Δ’ = 1 – 3 = -2 < 0
⇒ 3x2 – 2x + 1 > 0 ∀x ∈ R
b) Ta có:
a = -1 < 0
Δ’ = 4 – 1 = 3 > 0
Tam thức -x2 + 4x – 1 có hai nghiệm phân biệt \(x = 2 \pm \sqrt 3 \)
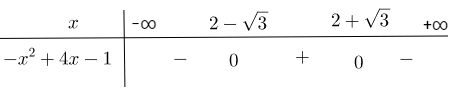
c) Ta có:
a = 1 > 0
Δ = 3 – 3 = 0
\({x^2} – \sqrt 3 x + {3 \over 4}\) có nghiệm kép \(x = {{\sqrt 3 } \over 2}\)
\( \Rightarrow {x^2} – \sqrt 3 x + {3 \over 4} > 0;\,\forall x \ne {{\sqrt 3 } \over 2}\)
d) Ta có:
\(\eqalign{
& a = 1 – \sqrt 2 < 0 \cr
& (1 – \sqrt 2 ){x^2} – 2x + 1 + \sqrt 2 = 0 \cr&\Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = – 3 – 2\sqrt 2 \hfill \cr} \right. \cr} \)
Advertisements (Quảng cáo)
Bảng xét dấu:

Bài 50: Tìm các giá trị của m để mỗi biểu thức sau luôn dương:
a) (m2+2)x2 – 2(m+1)x + 1
b) (m+2)x2 + 2(m+2)x + m + 3
a) Vì m2 + 2 > 0 nên (m2+2)x2 – 2(m+1)x + 1 > 0 ∀x ∈ R
⇔ Δ’ = (m + 1)2 – (m2 + 2) < 0 ⇔ 2m – 1< 0
\( \Leftrightarrow m < {1 \over 2}\)
Vậy với \(m < {1 \over 2}\) thì (m2+2)x2 – 2(m+1)x + 1 > 0 ∀ x ∈ R
b) Với \(m = -2\) thì ta có: \(f(x) = 1 >0, ∀x ∈\mathbb R\)
Với \(m ≠ -2\) ta có: \(f(x) > 0, ∀x ∈ R\)
\( \Leftrightarrow \left\{ \matrix{
a > 0 \hfill \cr
\Delta ‘ < 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
m + 2 > 0 \hfill \cr
{(m + 2)^2} – (m + 2)(m + 3) < 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
m > – 2 \hfill \cr
– m – 2 < 0 \hfill \cr} \right. \Leftrightarrow m > – 2\)
Advertisements (Quảng cáo)
Vậy \(f(x) > 0, ∀x ∈\mathbb R ⇔ m ≥ -2\)
Bài 51: Tìm các giá trị của m để mỗi biểu thức sau luôn âm.
a) \( – {x^2} + 2m\sqrt 2 x – 2{m^2} – 1\)
b) \(\left( {m – 2} \right){\rm{ }}{x^2} – {\rm{ }}2\left( {m – 3} \right)x{\rm{ }} + {\rm{ }}m{\rm{ }}-{\rm{ }}1\)
a) Vì \(a = -1 < 0\) nên:
\(\eqalign{
& – {x^2} + 2m\sqrt 2 x – 2{m^2} – 1 < 0\,\forall x \in R \cr
& \Leftrightarrow \Delta ‘ = 2{m^2} – (2{m^2} + 1) < 0 \cr
& \Leftrightarrow – 1 < 0 \cr} \)
Ta thấy điều suy ra luôn đúng
Vậy với mọi m thì \( – {x^2} + 2m\sqrt 2 x – 2{m^2} – 1 < 0; ∀x ∈\mathbb R \)
b) Đặt \(f(x) = \left( {m – 2} \right){\rm{ }}{x^2} – {\rm{ }}2\left( {m – 3} \right)x{\rm{ }} + {\rm{ }}m{\rm{ }}-{\rm{ }}1\)
+ Với \(m = 2\) thì \(f(x) = 2x + 1\) không thỏa mãn điều kiện yêu cầu bài toán
+ Với \(m ≠ 2\) thì: \(f(x) < 0, ∀x ∈\mathbb R \)
\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
a < 0 \hfill \cr
\Delta ‘ < 0 \hfill \cr} \right.\cr& \Leftrightarrow \left\{ \matrix{
m – 2 < 0 \hfill \cr
{(m – 3)^2} – (m – 2)(m – 1) < 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
m < 2 \hfill \cr
– 3m + 7 < 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
m < 2 \hfill \cr
m > {7 \over 3} \hfill \cr} \right. \cr} \)
Ta không tìm được m thỏa mãn hệ thức trên
Do đó, không có giá trị nào của m để \(f(x) < 0; ∀x ∈\mathbb R\)
Bài 52: Chứng minh định lý về dấu của tam thức bậc 2.
 Với các trường hợp Δ < 0 và Δ = 0, sử dụng hệ thức đã biết:
Với các trường hợp Δ < 0 và Δ = 0, sử dụng hệ thức đã biết:
\(f(x) = a{\rm{[(x}}\,{\rm{ + }}{b \over {2a}}{)^2} – {\Delta \over {4{a^2}}}{\rm{]}}\)
Hay \(af(x) = {a^2}[{(x + {b \over {2a}})^2} – {\Delta \over {4{a^2}}}]\)
Trong trường hợp Δ > 0, sử dụng hệ thức đã biết:
f(x) = a(x – x1)(x – x2) hay af(x) = a2(x – x1)(x – x2)
trong đó, x1 và x2 là hai nghiệm của tam thức bậc hai f(x)
Đáp án
Ta có: \(af(x) = {a^2}[{(x + {b \over {2a}})^2} – {\Delta \over {4{a^2}}}]\)
+ Nếu Δ < 0 thì af(x) > 0 với mọi x ∈ R, tức f(x) cùng dấu với a với mọi x ∈ R
+ Nếu Δ = 0 thì \(af(x) = {a^2}{(x + {b \over {2a}})^{^2}}\) khi đó af(x) > 0 với mọi \(x \ne – {b \over {2a}}\)
+ Nếu Δ > 0 thì f(x) có hai nghiệm phân biệt x1 và x2 và:
f(x) = a(x – x1)(x – x2)
Do đó: af(x) = a2(x – x1)(x – x2)
Vậy af(x) có cùng dấu với tích (x – x1)(x – x2).
Dấu của tích này được cho trong bảng sau (x1 < x2)

Do đó: af(x) < 0 với mọi x ∈ (x1, x2)
Và af(x) > 0 với mọi x < x1 hoặc x > x2

