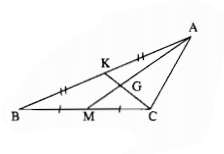
Câu 31: Cho hình bên. Điền vào chỗ trống:
GK = ….CK; AG = … GM; GK = … CG;
AM = ….AG; AM = … GM.
\(GK = {1 \over 3}CK;AG = 2GM\)
\(GK = {1 \over 2}CG;AM = {3 \over 2}AG\)
AM = 3GM
Câu 32: Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
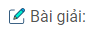
Giả sử ∆ABC có hai đường trung tuyến BD, CE và BD = CE. Gọi G là giao điểm BD và CE.
\(BG = {2 \over 3}B{\rm{D}}\) (tính chất đường trung tuyến)
\(CG = {2 \over 3}CE\) (tính chất đường trung tuyến)
Suy ra: BG = CG
BD = CE
\( \Rightarrow \) BG + GD = CG + GE
Xét ∆BGE và ∆CGD:
BG = CG (chứng minh trên)
\(\widehat {BGE} = \widehat {CG{\rm{D}}}\) (đối đỉnh)
GE = GD (chứng minh trên)
Do đó: ∆BGE = ∆CGD (c.g.c)
\( \Rightarrow \) BE = CD (1)
\(BE = {1 \over 2}AB\) (Vì E là trung điểm AB) (2)
\(C{\rm{D = }}{1 \over 2}AC\) (Vì D là trung điểm AC) (3)
Từ (1), (2) và (3) suy ra: AB = CD.Vậy ∆ABC cân tại A.
Câu 33: Tam giác ABC cân tại A có AB = AC = 34cm, BC = 32cm. Kẻ đường trung tuyến AM.
a) Chứng minh rằng \(AM \bot BC\)
b) Tính độ dài AM.
Advertisements (Quảng cáo)
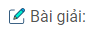
a) Xét ∆AMB và ∆AMC:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Do đó: ∆AMB = ∆AMC (c.c.c)
\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (1)
Ta có: \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù) (2)
Từ (1) và (2) suy ra: \(\widehat {AMB} = \widehat {AMC} = 90^\circ \)
Vậy: \(AM \bot BC\)
b) Xét tam giác vuông AMB ta có: \(\widehat {AMB} = 90^\circ \)
Theo định lý Pitago ta có:
$$\eqalign{
& \,\,\,\,A{B^2} = A{M^2} + B{M^2} \cr
& \Rightarrow A{M^2} = A{B^2} – B{M^2} = {34^2} – {16^2} \cr
& \,\,\,\,\,A{M^2} = 1156 – 256 = 900 \cr
& \Rightarrow AM = 30\left( {cm} \right) \cr} $$
Câu 34: Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:
a) Các cạnh của tam giác BGD bằng \({2 \over 3}\) các đường trung tuyến của tam giác ABC
b) Các đường trung tuyến của tam giác BGD bằng một nửa các cạnh của tam giác ABC.
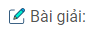
Advertisements (Quảng cáo)
a) Gọi AM, BN, CP là các đường trung tuyến của ∆ABC cắt nhau tại G.
AG = GD (gt)
AG = 2GM (suy ra từ tính chất đường trung tuyến)
Nên GD = 2GM
GD = GM + MD
Suy ra: GM = MD
Xét ∆BMD và ∆CMG:
BM = CM (gt)
\(\widehat {BM{\rm{D}}} = \widehat {CMG}\) (đối đỉnh)
MD = GM (chứng minh trên)
Do đó: ∆BMD = ∆CMG (c.g.c)
\( \Rightarrow \) BD = CG
\(CG = {2 \over 3}CP\) (tính chất đường trung tuyến)
Suy ra: \(B{\rm{D = }}{2 \over 3}CP\) (1)
\(BG = {2 \over 3}BN\) (tính chất đường trung tuyến) (2)
\({\rm{A}}G = {2 \over 3}AM\) (tính chất đường trung tuyến)
Suy ra: \(G{\rm{D}} = {2 \over 3}AM\) (3)
Từ (1), (2) và (3) suy ra các cạnh của ∆BGD bằng \({2 \over 3}\) các đường trung tuyến của ∆ABC.
b) GM = MD (chứng minh trên)
nên BM = MD là đường trung tuyến của ∆BGD
\(BM = {1 \over 2}BC\) (4)
Kẻ đường trung tuyến GE và DF của ∆BGD
\( \Rightarrow FG = {1 \over 2}BG\)
\(GN = {1 \over 2}BG\) (tính chất đường trung tuyến)
Nên FN = GN
Xét ∆DFG và ∆ANG:
AG = GD (gt)
\(\widehat {DGF} = \widehat {AGN}\) (đối đỉnh)
GF = GN (chứng minh trên)
Do đó ∆DFG = ∆ANG (c.g.c)
\( \Rightarrow \) DF = AN
\(AN = {1 \over 2}AC\) (gt)
Suy ra: \({\rm{D}}F = {1 \over 2}AC\) (5)
BD = CG (chứng minh trên)
\({\rm{ED}} = {1 \over 2}B{\rm{D}}\) (Vì E là trung điểm BD)
\(GP = {1 \over 2}CG\) (tính chất đường trung tuyến)
Suy ra: ED = GP
∆BDM = ∆CGM (chứng minh trên)
\( \Rightarrow \widehat {B{\rm{D}}M} = \widehat {CGM}\) hay \(\widehat {E{\rm{D}}G} = \widehat {CGM}\)
\(\widehat {CGM} = \widehat {PGA}\) (đối đỉnh)
Suy ra: \(\widehat {{\rm{ED}}G} = \widehat {PGA}\)
AG = GD (gt)
Suy ra: ∆PGA = ∆EDG (c.g.c)=> GE = AP mà
Suy ra: \(GE = {1 \over 2}AB\) (6)
Từ (4),(5) và (6) suy ra các đường trung tuyến của ∆BGD bằng một nửa cạnh của ∆ABC.

