Câu 35: Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE < 15cm.
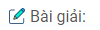
Gọi G là giao điểm của 2 đường trung tuyến BD và CE.
Trong ∆GBC ta có:
GB + GC > BC (bất đẳng thức tam giác)
\(GB = {2 \over 3}B{\rm{D}}\) (tính chất đường trung tuyến)
\(GC = {2 \over 3}CE\) (tính chất đường trung tuyến)
BC = 10cm (gt)
Suy ra: \({2 \over 3}\left( {B{\rm{D}} + CE} \right) > 10 \)
\(\Rightarrow B{\rm{D}} + CE > 10:{2 \over 3} = 10.{3 \over 2} = 15\)
Vây BD + CE > 15 (cm)
Câu 36: Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho \(BE = {1 \over 3}BC\). Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.
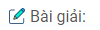
Trong ∆ACD ta có CB là đường trung tuyến kẻ từ đỉnh C.
E ∈ BC và \(BE = {1 \over 3}BC\) (gt)
Suy ra: \(CE = {2 \over 3}CB\) nên E là trọng tâm của ∆ACD.
Do đó AK là đường trung tuyến của ∆ACD.
Xuất phát từ đỉnh A nên K là trung điểm của CD.
Vậy KD = KC.
Câu 37: Theo kết quả của bài 64 chương II, SBT Toán 7 tập 1 ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:
Advertisements (Quảng cáo)
a) IK // DE, IK = DE
b) \({\rm{A}}G = {2 \over 3}A{\rm{D}}\)
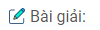
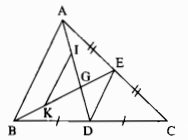
a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 vào ∆ABC vào ∆AGB ta có:
DE // AB và \({\rm{D}}E = {1 \over 2}AB\) (1)
IK // AB và \(IK = {1 \over 2}AB\) (2)
Từ (1) và (2) suy ra: DE // IK và DE // IK
b) AD và BE là 2 đường trung tuyến của ∆ABC cắt nhau tại G.
\( \Rightarrow AG = {2 \over 3}AD\) (tính chất đường trung tuyến)
Câu 38: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm M sao cho MD = MA.
a) Tính số đo góc ABD.
b) Chứng minh: ∆ABC = ∆BAD.
c) So sánh độ dài AM và BC.
Advertisements (Quảng cáo)
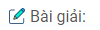
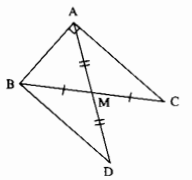
a) Xét ∆AMC và ∆BMD:
BM = MC (gt)
\(\widehat {ABM} = \widehat {BMC}\) (đối đỉnh)
AM = MD (gt)
Do đó: ∆AMC = ∆DMB (c.g.c)
\( \Rightarrow \widehat {MAC} = \widehat D\) (2 góc tương ứng)
Suy ra: AC // BD (vì có hai góc ở vị trí so le trong bằng nhau)
\(AB \bot AC\left( {gt} \right)\)
Suy ra \(AB \bot B{\rm{D}}\). Vậy \(\widehat {AB{\rm{D}}} = 90^\circ \)
b) Xét ∆ABC và ∆BAD:
AB cạnh chung
\(\widehat {BAC} = \widehat {AB{\rm{D}}} = 90^\circ \)
AC = BD (Vì ∆AMC = ∆DMB)
Do đó: ∆ABC = ∆BAD (c.g.c)
c) ∆ABC = ∆BAD => BC = AD (2 cạnh tương ứng)
Ta có: \(AM = {1 \over 2}A{\rm{D}}\). Suy ra: \({\rm{A}}M = {1 \over 2}BC\)
Câu 39: Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng \(\widehat {BAC} = 90^\circ \).
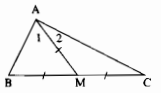
Ta có AM là đường trung tuyến của ∆ABC.
\( \Rightarrow BM = MC = {1 \over 2}BC\)
\(AM = {1 \over 2}BC\left( {gt} \right)\)
Suy ra: AM = BM = MC
∆AMB có AM = MB nên ∆AMB cân tại M.
\( \Rightarrow \widehat B = \widehat {{A_1}}\) (tính chất tam giác cân) (1)
∆AMC có AM = MC nên ∆AMC cân tại M.
\( \Rightarrow \widehat C = \widehat {{A_2}}\) (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: \(\widehat B + \widehat C = \widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAC}\) (3)
Trong ∆ABC ta có:
\(\widehat B + \widehat C + \widehat {BAC} = 180^\circ \) (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: \(\widehat {BAC} + \widehat {BAC} = 180^\circ \)
\( \Rightarrow 2\widehat {BAC} = 180^\circ \Rightarrow \widehat {BAC} = 90^\circ \)
Vậy ∆ABC vuông tại A.

