Bài 61: Tìm tập xác định của mỗi hàm số sau:
a) \(y = \sqrt {(2x + 5)(1 – 2x)} \)
b) \(y = \sqrt {{{{x^2} + 5x + 4} \over {2{x^2} + 3x + 1}}} \)
Đáp án
a) Hàm số đã cho xác định
\(⇔ (2x + 5)(1 – 2x) ≥ 0\)
\( \Leftrightarrow – {5 \over 2} \le x \le {1 \over 2}\)
Vậy tập xác định \(D = {\rm{[}} – {5 \over 2},{1 \over 2}{\rm{]}}\)
b) Hàm số đã cho xác định:
\(\eqalign{
& \Leftrightarrow {{{x^2} + 5x + 4} \over {2{x^2} + 3x + 1}} \ge 0 \Leftrightarrow {{(x + 1)(x + 4)} \over {(x + 1)(2x + 1)}} \ge 0 \cr
& \Leftrightarrow \left\{ \matrix{
x \ne – 1 \hfill \cr
{{x + 4} \over {2x + 1}} \ge 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ne – 1 \hfill \cr
\left[ \matrix{
x \le – 4 \hfill \cr
x > – {1 \over 2} \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x \le – 4 \hfill \cr
x > – {1 \over 2} \hfill \cr} \right. \cr} \)
Vậy tập xác định của hàm số là: \(S = ( – \infty , – 4{\rm{]}} \cup ( – {1 \over 2}, + \infty )\)
Bài 62: Giải các hệ bất phương trình
a)
\(\left\{ \matrix{
4x – 3 < 3x + 4 \hfill \cr
{x^2} – 7x + 10 \le 0 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
2{x^2} + 9x – 7 > 0 \hfill \cr
{x^2} + x – 6 \le 0 \hfill \cr} \right.\)
c)
Advertisements (Quảng cáo)
\(\left\{ \matrix{
{x^2} – 9 < 0 \hfill \cr
(x – 1)(3{x^2} + 7x + 4) \ge 0 \hfill \cr} \right.\)
Đáp án
a) Ta có:
\( \Leftrightarrow \left\{ \matrix{
4x – 3 < 3x + 4 \hfill \cr
{x^2} – 7x + 10 \le 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x < 7 \hfill \cr
2 \le x \le 5 \hfill \cr} \right.\)
\(\Leftrightarrow 2 \le x \le 5\)
Vậy \(S = [2, 5]\)
b) Ta có:
\(\eqalign{
& \left\{ \matrix{
2{x^2} + 9x – 7 > 0 \hfill \cr
{x^2} + x – 6 \le 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\left[ \matrix{
x < {{ – 9 – \sqrt {137} } \over 4} \hfill \cr
x > {{ – 9 + \sqrt {137} } \over 4} \hfill \cr} \right. \hfill \cr
– 3 \le x \le 2 \hfill \cr} \right. \cr
& \Leftrightarrow {{ – 9 + \sqrt {137} } \over 4} < x < 2 \cr} \)
Vậy \(S = ({{ – 9 + \sqrt {137} } \over 4};2{\rm{]}}\)
c) Ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& \left\{ \matrix{
{x^2} – 9 < 0 \hfill \cr
(x – 1)(3{x^2} + 7x + 4) \ge 0 \hfill \cr} \right.\cr& \Leftrightarrow \left\{ \matrix{
– 3 < x < 3 \hfill \cr
\left[ \matrix{
– {4 \over 3} \le x \le – 1 \hfill \cr
x \ge 1 \hfill \cr} \right. \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
– {4 \over 3} \le x \le – 1 \hfill \cr
1 \le x \le 3 \hfill \cr} \right. \cr} \)
Vậy \(S = \,{\rm{[}} – {4 \over 3},\, – 1{\rm{]}}\, \cup {\rm{[}}1,\,3)\)
Bài 63: Tìm các giá trị của a sao cho với mọi x, ta luôn có:
\( – 1 \le {{{x^2} + 5x + a} \over {2{x^2} – 3x + 2}} < 7\)
Đáp án
Vì 2x2 – 3x + 3 > 0 ∀x ∈ R (do a = 3 > 0; Δ = -15 < 0)
Nên:
\(\eqalign{
& – 1 \le {{{x^2} + 5x + a} \over {2{x^2} – 3x + 2}} < 7 \cr&\Leftrightarrow – 2{x^2} + 3x – 2 \le {x^2} + 5x + a < \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;7(2{x^2} – 3x + 2) \cr
& \Leftrightarrow \left\{ \matrix{
3{x^2} + 2x + a + 2 \ge 0 \hfill \cr
13{x^2} – 26x – a + 14 > 0 \hfill \cr} \right.\,\,\,\,\,\,\,\,\,\,\,\,(1) \cr} \)
Hệ (1) tương đương với mọi x:
\( \Leftrightarrow \left\{ \matrix{
\Delta {‘_1} = 1 – 3(a + 2) \le 0 \hfill \cr
\Delta {‘_2} = 169 – 13(14 – a) < 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
3a \ge – 5 \hfill \cr
13a < 13 \hfill \cr} \right. \Leftrightarrow – {5 \over 3} \le a < 1\)
Bài 64:Tìm các giá trị của m để hệ bất phương trình sau có nghiệm:
\(\left\{ \matrix{
{x^2} + 2x – 15 < 0 \hfill \cr
(m + 1)x \ge 3 \hfill \cr} \right.\)
Đáp án
Ta có: x2 + 2x – 15 < 0 ⇔ -5 < x < 3
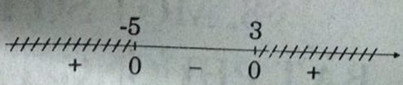
Ta xét bất phương trình: (m + 1)x ≥ 3 (*)
+ Nếu m = -1 thì S = Ø
+ Nếu m > -1 thì: \((*) \Leftrightarrow x \ge {3 \over {m + 1}}\)
Hệ có nghiệm:
\( \Leftrightarrow \left\{ \matrix{
{3 \over {m + 1}} < 3 \hfill \cr
m > – 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
m > 0 \hfill \cr
m > – 1 \hfill \cr} \right. \Leftrightarrow m > 0\)
+ Nếu m < -1 thì \((*) \Leftrightarrow x \le {3 \over {m + 1}}\)
Hệ có nghiệm:
\( \Leftrightarrow \left\{ \matrix{
{3 \over {m + 1}} > – 5 \hfill \cr
m + 1 < 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
3 < – 5m – 5 \hfill \cr
m < – 1 \hfill \cr} \right. \Leftrightarrow m < – {8 \over 5}\)
Vậy hệ có nghiệm khi và chỉ khi:
\(\left[ \matrix{
m < – {8 \over 5} \hfill \cr
m > 0 \hfill \cr} \right.\)

