Bài 26.8: Ba môi trường trong suốt (1), (2), (3) có thể đặt tiếp giáp nhau. Với cùng góc tới i = 60° ; nếu ánh sáng truyền từ (1) vào (2) thì góc khúc xạ là 45°; nếu ánh sáng truyền từ (1) vào (3) thì góc khúc xạ là 30°. Hỏi nếu ánh sáng truyền từ (2) vào (3) vẫn với góc tới i thì góc khúc xạ là bao nhiêu ?
Theo đề ra: n1sin600 = n2sin450 = n3sin300
Ta phải tìm r3 nghiệm đúng phương trình: n2sin600 = n3sinr3
\(\eqalign{
& \Rightarrow {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_3} = {{{n_2}} \over {{n_3}}}\sin {60^0} = {{\sin {{30}^0}} \over {\sin {{45}^0}}}.\sin {60^0} \cr
& \Rightarrow {r_3} \approx {38^0} \cr} \)
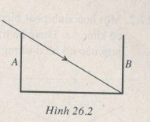
Bài 26.9: Một cái máng nước sâu 30 cm, rộng 40 cm có hai thành bên thẳng đứng. Đúng lúc máng cạn nước thì có bóng râm của thành A kéo dài tới đúng chân thành B đối diện (Hình 26.2). Người ta đổ nước vào máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = 4/3. Hãy tính h và vẽ tia sáng giới hạn bóng râm của thành máng khi có nước.
Advertisements (Quảng cáo)
CC’ = 7cm
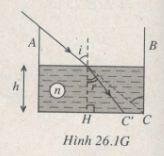–> HC – HC’ = h(tani – tanr) = 7cm (Hình 26.1G).
\(\eqalign{
& \tan i = {4 \over 3};{\mathop{\rm t}\nolimits} {\rm{anr}} = {{{\mathop{\rm s}\nolimits} {\rm{inr}}} \over {{\rm{cosr}}}};{\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n} = {3 \over 5} \cr
& {\rm{cosr = }}\sqrt {1 – {{\sin }^2}r} = {4 \over 5};{\mathop{\rm t}\nolimits} {\rm{anr}} = {3 \over 4} \cr} \)
Do đó:
\(h\left( {{4 \over 3} – {3 \over 4}} \right) = 7cm \Rightarrow h = 12cm\)
Advertisements (Quảng cáo)
Bài 26.10: Một dải sáng đơn sắc song song chiếu tới mặt chất lỏng với góc tới i. Chất lỏng có chiết suất n. Dải sáng nằm trong một mặt phẳng vuông góc với mặt chất lỏng. Bề rộng của dải sáng trong không khí là d.
Lập biểu thức bề rộng đ của dải sáng trong chất lỏng theo n, i, d.
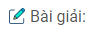
Ta có (HÌnh 26.2G):
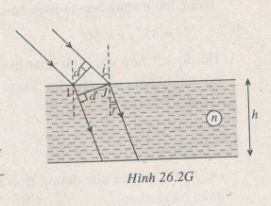
d = IJcosi; d’ = Ijcosr
Suy ra: \(d’ = {{{\rm{cosr}}} \over {{\rm{cosi}}}}d\)
Nhưng:
\({\mathop{\rm cosr}\nolimits} = \sqrt {1 – {{\sin }^2}r} = \sqrt {1 – {{{{\sin }^2}i} \over {n{}^2}}} = {{\sqrt {{n^2} – {{\sin }^2}i} } \over {n\cos i}}d\)
Do đó:
\({\rm{d}}’ = {{\sqrt {{n^2} – {{\sin }^2}i} } \over {n\cos i}}d\)
