Bài VI.6: Nếu muốn có phản xạ toàn phần thì (các) điều kiện là:
A. (1) B. (2) C. (1) và (4) D. (2) và (3)
Đáp án D
Bài VI.7: Một thợ lặn ở dưới nước nhìn thấy Mặt Trời ở độ cao 60° so với đường chân trời. Tính độ cao thực của Mặt Trời so với đường chân trời. Biết chiết suất của nước là n = 4/3.
Hướng của Mặt Trời mà người thợ lặn nhìn thấy là hướng của các tia sáng khúc xạ vào nước.
Ta có đường đi của các tia sáng như hình VI.1G:
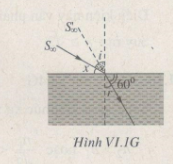
Do đó: r = 900 – 600 = 300
–> sini = nsinr = (4/3)sin300 = 2/3
–> i ≈ 420
Độ cao thực của Mặt Trời so với đường chân trời:
x = 900 – i = 480
Advertisements (Quảng cáo)
Bài VI.8: Một cái gậy dài 2m cắm thẳng đứng ở đáy hồ. Gậy nhô lên khỏi mật nước 0,5 m. Ánh sáng Mặt Trời chiếu xuống hồ theo phương hợp với pháp tuyến của mặt nước góc 60°. Tìm chiều dài bóng của cây gậy in trên đáy hồ.
Bóng của cây gậy trên đáy hồ được biểu thị bởi đoạn BB” (Hình VI.2G)
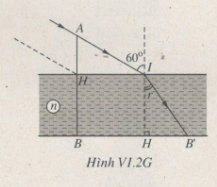
BB’ = BH + HB’ = HI + HB’ = AH.tani + HB.tanr
Định luật khúc xạ:
\(\eqalign{
& {\mathop{\rm sinr}\nolimits} = {{\sin i} \over n};co{\rm{sr = }}{{\sqrt {{n^2} – {{\sin }^2}i} } \over n} \cr
& {\mathop{\rm t}\nolimits} {\rm{anr}} = {{\sin i} \over {\sqrt {{n^2} – {{\sin }^2}i} }} = 0,854 \cr} \)
Do đó: BB’ = 0,5.1,73 + 1,5.0,854 – 2,15m
Advertisements (Quảng cáo)
Bài VI.9: Một khối nhựa trong suốt hình lập phương, chiết suất n (Hình VI.3). Xác định điều kiện về n để mọi tia sáng từ không khí khúc xạ vào một mặt và truyền thẳng tới mặt kề đều phản xạ toàn phần ở mặt này.
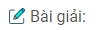
Điều kiện i2 ≥ igh à sini2 ≥ 1/n
Nhưng: sini2 = cosr1; sinr1 = (1/n)sini1
Vậy:
\(\eqalign{
& {{\sqrt {{n^2} – {{\sin }^2}{i_1}} } \over n} \ge {1 \over n} \cr
& {n^2} \ge 1 + {\sin ^2}{i_1} \cr} \)
Điều kiện này vẫn phải nghiệm với i1 max = 900
Suy ra \(n \ge \sqrt 2 \)
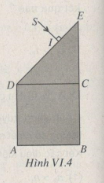
Bài VI.10: Một khối trong suốt có tiết diện thẳng như Hình VI.4, đặt trong không khí (ABCD là hình vuông ; CDE là tam giác vuông cân). Trong mặt phẳng của tiết diện thẳng, chiếu một chùm tia sáng đơn sắc hẹp SI vuông góc với DE (IE < ID).
Giả sử phần CDE có chiết suất n1 = 1,5 và phần ABCD có chiết suất n2 n1 tiếp giáp nhau.
Hãy tính n2 để tia khúc xạ trong thuỷ tinh tới mặt AD sẽ ló ra không khí theo phương hợp với SI một góc 450.
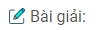
Xem hình VI.4G.
Tại J’ phải có khúc xạ:
n2 > n1 hoặc \({{{n_1}} \over {\sqrt 2 }} < {n_2} < {n_1}\)
Vì i + r = 900 nên có thể thiết lập hệ thức liên hệ giữa n2 và n1 theo điều kiện tại K.
Do đó r = 450 –> n2 = 1,275

