Câu 1: Viết tỉ số của các cặp đoạn thẳng sau:
a. AB = 125cm, CD = 625 cm;
b. EF = 45cm, E’F’ = 13,5dm
c. MN = 555cm, M’N’ = 999cm
d. PQ = 10101cm, P’Q’ = 303,03m
a. Ta có:
\({{AB} \over {CD}} = {{125} \over {625}} = {1 \over 5}\)
b. Đổi: E’F’ = 13,5dm = 135 cm
Ta có:
\({{EF} \over {E’F’}} = {{45} \over {135}} = {1 \over 3}\)
c. Ta có:
\({{MN} \over {M’N’}} = {{555} \over {999}} = {{111.5} \over {111.9}} = {5 \over 9}\)
d. Đổi: P’Q’ = 303,03m = 30303cm
Ta có:
\({{PQ} \over {P’Q’}} = {{10101} \over {30303}} = {{10101} \over {10101.3}} = {1 \over 3}\)
Câu 2: Đoạn thẳng AB gấp năm lần đoạn thẳng CD; đoạn thẳng A’B’ gấp bảy lần đoạn thẳng CD.
a. Tính tỉ số của hai đoạn thẳng AB và A’B’
b. Cho biết đoạn thẳng MN = 505cm và đoạn thẳng M’N’ = 707cm, hỏi hai đoạn thẳng AB , A’B’ có tỉ lệ với hai đoạn thẳng MN và M’N’ hay không ?
a. Chọn đoạn thẳng CD làm đơn vị
Advertisements (Quảng cáo)
Suy ra đoạn thẳng AB = 5 (đơn vị), đoạn thẳng A’B’ = 7 (đơn vị).
Vậy: \({{AB} \over {A’B’}} = {5 \over 7}\)
b. Ta có:
\({{MN} \over {M’N’}} = {{505} \over {707}} = {{101.5} \over {101.7}} = {5 \over 7}\)
Vì \({{AB} \over {A’B’}} = {{MN} \over {M’N’}}\) nên AB và A’B’ tỉ lệ với MN và M’N’.
Câu 3: Tính độ dài x của các đoạn thẳng trong hình 1, biết rằng các số trên hình cùng đơn vị đo là cm.
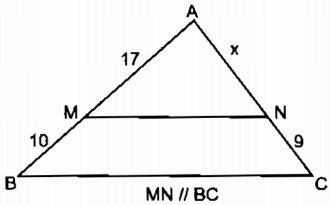
a. Xem hình 1
Trong ∆ ABC, ta có: MN // BC
Suy ra: \({{AM} \over {MB}} = {{AN} \over {NC}}\) (định lí Ta –lét)
Hay \({{17} \over {10}} = {x \over 9}\)
Advertisements (Quảng cáo)
Vậy \(x = {{17.9} \over {10}} = 15,3\) (cm)
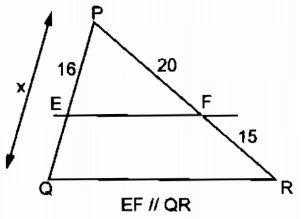
b. Xem hình 2
Trong ∆ PQR, ta có: EF // QR
Suy ra: \({{EP} \over {PQ}} = {{PF} \over {PR}}\)
Hay \({{16} \over x} = {{20} \over {PR}}\)
Mà \(PR = PF + FR = 20 + 15 = 35\)
Vậy \(x = {{16.35} \over {20}} = 28\) (cm)
Câu 4: Cho hình thang ABCD có AB // CD và AB < CD
Đường thẳng song song với đáy AB cắt các cạnh bên CD, BC theo thứ tự tại M và N.
Chứng minh rằng:
a. \({{MA} \over {AD}} = {{NB} \over {BC}}\)
b. \({{MA} \over {MD}} = {{NB} \over {NC}}\)
c. \({{MD} \over {DA}} = {{NC} \over {CB}}\)
HD: Kéo dài các tia DA, CB cắt nhau tại E(h.3), áp dụng định lí Ta-lét trong tam giác và tính chất của tỉ lệ thức để chứng minh.
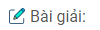
(xem hình 3)
a. Gọi E là giao điểm của AD và BC.
Trong ∆ EMN, ta có: AB // MN (gt)
Suy ra: \({{EA} \over {MA}} = {{EB} \over {NB}}\) (định lí Ta-lét)
Hay \({{EA} \over {EB}} = {{MA} \over {NB}}\) (1)
Trong ∆ EDC, ta có: AB // CD (gt)
Suy ra: \({{EA} \over {AD}} = {{EB} \over {BC}}\) (định lí Ta-lét)
Hay \({{EA} \over {EB}} = {{AD} \over {BC}}\) (2)
Từ (1) và (2) suy ra: \({{MA} \over {NB}} = {{AD} \over {BC}} \Rightarrow {{MA} \over {AD}} = {{NB} \over {BC}}\)
b. Ta có: \({{MA} \over {AD}} = {{NB} \over {BC}}\) (gt)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\({{MA} \over {AD – MA}} = {{NB} \over {BC – NB}} \Rightarrow {{MA} \over {MD}} = {{NB} \over {NC}}\)
c. Ta có: \({{MA} \over {MD}} = {{NB} \over {NC}}\) (gt)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\({{MA} \over {MD}} = {{NB} \over {NC}} \Rightarrow {{MD} \over {MA + MD}} = {{NC} \over {NB + NC}} \Rightarrow {{MD} \over {DA}} = {{NC} \over {CB}}\)

