Câu 62: Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình 147 dưới đây (cạnh đáy và chiều cao bằng nhau):
(xem hình 147)
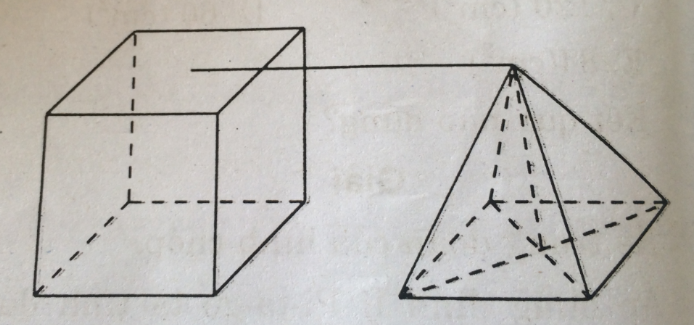
Nếu thể tích lăng trụ là V thì thể tích hình chóp là:
A. V
B. \({V \over 2}\)
C. \({V \over 3}\)
D. \({V \over 4}\)
Hãy chọn kết quả đúng.
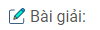
Một hình chóp tứ giác đều và một lăng trụ đứng đáy là tứ giác đều có chiều cao bằng nhau. Nếu thể tích của hình trụ là V thì thể tích hình chóp là \({V \over 3}\)
Vậy chọn đáp án C
Câu 63: Một cái nhà kính trồng cây thí nghiệm có dạng một lăng trụ đứng có các kích thước như ở hình 148. EDC là một tam giác cân. Hãy tính:
a. Diện tích hình ABCDE
b. Thể tích nhà kính
c. Diện tích kính cần phải có để “lợp” hai mái và bốn bức tường nhà (không tính riềm, mép, …)
(hình 148 trang 151 sbt)
a. Chia hình ABCDE thành hai hình thang vuông có cạnh đáy nhỏ là 5m, đáy lớn 8m, chiều cao là 4m.
Ta có: \({S_{ABCDE}} = 2.{{5 + 8} \over 2}.4 = 52({m^2})\)
b. Thể tích hình lăng trụ đứng (nhà kính) là :
V = S.h = 52.10 = 520 (m
Advertisements (Quảng cáo)
b. Thể tích hình lăng trụ đứng (nhà kính) là :
V = S.h = 52.10 = 520 (m3)
c. Diện tích nhà kính gồm bốn hình chữ nhật có kích thước là 5m và 10m và hai hình bằng diện tích hình ABCDE.
Diện tích bốn hình chữ nhật là: (5.10).4 = 200 (m2)
Tổng diện tích kính cần dùng là: 200 + 52.2 = 304 (m2)
Câu 64: Hình 149 là chiếc lều ở một trại hè với các kích thước cho trên hình.
a. Tính thể tích của lều.
b. Số vải bạt cần phải có để dựng lều đó là bao nhiêu ?
(Không tính các mép gấp đường viền, v.v…)
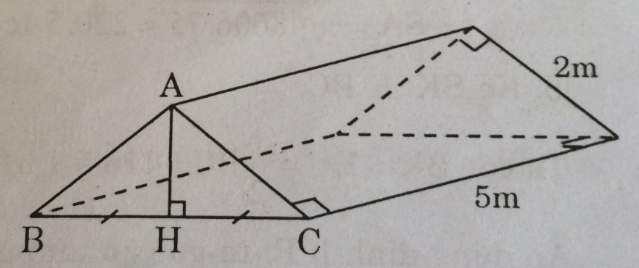
(hình 149 trang 151 sbt)
a. Lều là lăng trụ đứng đáy tam giác vuông cân, cạnh 2m, chiều cao lăng trụ 5m.
Diện tích đáy là:
Advertisements (Quảng cáo)
Sđáy \( = {1 \over 2}.2.2 = 2({m^2})\)
Thể tích lều là:
V = S.h = 2.5 = 10 (m3)
b. Số vải cần để làm lều là hai mặt bên và hai đầu hồi (hai đáy của lăng trụ đứng).
Diện tích hai mặt bên là: (2.5).2 = 20 (m2)
Diện tích vải cần dùng là: 20 + 2.2 = 24 (m2)
Câu 65
1. Kim tự tháp Kê-ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m, chiều cao hình chóp 146,5m.
a. Độ dài cạnh bên là bao nhiêu ?
b. Tính diện tích xung quanh của hình chóp.
c. Tính thể tích hình chóp.
2. Kim tự tháp Lu-vrơ (Louvre) (Xây dựng vào năm 1988).
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-vrơ (Pháp). Mô hình có dạng chóp đều chiều cao 21m, độ dài cạnh đáy là 34m.
a. Cạnh bên của hình chóp là bao nhiêu ?
b. Tính thể tích hình chóp.
c. Tính tổng diện tích các tấm kính để phủ lên hình chóp này (Sxq).
(hình trang 158 sgbt)
Giả sử các kim tự tháp là hình chóp tứ giác đều S.ABCD.
a. Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:
\(O{A^2} + O{B^2} = A{B^2}\)
Suy ra: \(2.O{A^2} = A{B^2}\)
Suy ra: \(O{A^2} = {{A{B^2}} \over 2} = 27144,5\)
Áp dụng định lí Pi-ta-go vào tam giác vuông SOA, ta có:
\(\eqalign{ & S{A^2} = S{O^2} + O{A^2} \cr & = 146,{5^2} + 27144,{5^2} = 48606,75 \cr & SA = \sqrt {48606,75} \approx 220,5(cm) \cr} \)
b. Kẻ SK ⊥ BC.
Ta có: \(BK = KC = {1 \over 2}BC = 116,5(m)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông SIB, ta có:
\(S{B^2} = S{K^2} + B{K^2}\)
Suy ra:
\(\eqalign{ & S{K^2} = S{B^2} – B{K^2} \cr & = 48606,75 – 13572,25 = 35034,5 \cr & SK = \sqrt {35034,5} \cr} \)
Diện tích xung quanh của kim tự tháp là:
\(S = \left( {233.2} \right).\sqrt {35034,5} \approx 87223,6({m^2})\)
Thể tích hình chóp là:
\(V = {1 \over 3}S.h = {1 \over 3}.233.233.146,5 = 2651112,8({m^3})\)
2. Tương tự câu 1, trong đó tổng diện tích các tấm kính để phủ lên hình chóp chính là diện tích xung quanh của hình chóp.

