Câu 11.1: Cạnh của một hình thoi bằng 25, một đường chéo bằng 14. Đường chéo kia bằng:
A. 24
B. 48
C. \(\sqrt {429} \)
D. Một đáp số khác.
Hãy chọn phương án đúng
Chọn B. 48 đúng
Câu 11.2: Cho hình thang cân ABCD( AB // CD). Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?
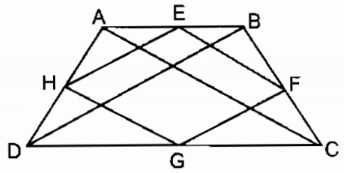
Trong ∆ ABD ta có:
E là trung điểm của AB (gt)
H là trung điểm của AD (gt)
nên EH là đường trung bình của ∆ ABD
Advertisements (Quảng cáo)
⇒ EH // BD và EH = \({1 \over 2}\)BD (tính chất đường trung bình của tam giác) (1)
– Trong ∆ CBD ta có:
F là trung điểm của BC (gt)
G là trung điểm của CD (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD và FG = \({1 \over 2}\)BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EH // FG và EH = FG
Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Advertisements (Quảng cáo)
Trong ∆ ABC ta có:
EF là đường trung bình
⇒ EF = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) (3)
AC = BD (tính chất hình thang cân) (4)
Từ (1), (3) và (4) suy ra: EH = EF
Vậy : Tứ giác EFGH là hình thoi.
Câu 11.3: Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ đường thẳng song song với AC, cắt AB ở I. Qua D kẻ đường thẳng song song với AB, cắt AC ở K.
a. Tứ giác AIDK là hình gì ?
b. Điểm D ở vị trí nào trên cạnh BC thì AIDK là hình thoi ?
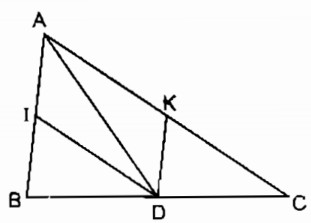
a. Ta có: DK // AB (gt)
hay DK // AI
DI // AC (gt)
hay DI // AK
Vậy tứ giác AIDK là hình bình hành
b. Để hình bình hành AIDK là hình thoi.
⇒ AD là đường phân giác \(\widehat {IAK}\)
hay AD là đường phân giác \(\widehat {BAC}\)
Ngược lại nếu AD là tia phân giác \(\widehat {BAC}\)
Ta có tứ giác AIDK là hình bình hành có đường chéo AD là phân giác của góc A nên tứ giác AIDK là hình thoi
Vậy hình bình hành AIDK là hình thoi khi và chỉ khi D là giao điểm tia phân giác của góc A và cạnh BC.

