Câu 10.1: Tập hợp giao điểm hai đường chéo của hình chữ nhật ABCD có A và B cố định là
A. Đường trung trực của AD;
B. Đường trung trực của AB;
C. Đường trung trực của BC;
D. Đường tròn (A; AB)
Hãy chọn phương án đúng.
Chọn B. Đường trung trực của AB. Đúng
Câu 10.2: Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
Advertisements (Quảng cáo)

Xét hai tam giác vuông MOA và MOB: \(\widehat {MAO} = \widehat {MBO} = {90^0}\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {AOM} = \widehat {BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat {AOM} = \widehat {BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Câu 10.3: Xét các hình bình hành ABCD có cạnh AD cố định, cạnh AB = 2cm. Gọi I là giao điểm của AC và BD. Điểm I chuyển động trên đường nào ?
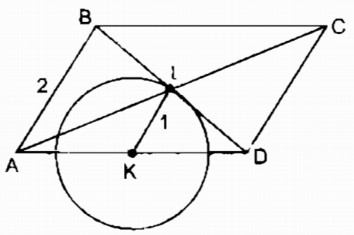
Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = \({1 \over 2}\)AB =\({1 \over 2}\).2 = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K ; 1 cm)

