Câu 161: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC.
a. Chứng minh rằng tứ giác DEHK là hình bình hành.
b. Tam giác ABC có điều kiện gì thì tứ giác DEHK là hình chữ nhật ?
c. Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì ?


a. Ta có: GD = \({1 \over 2}\)GB (tính chất đường trung tuyến của tam giác)
GH = \({1 \over 2}\)GB (gt)
Suy ra: GD = GH
GE = \({1 \over 2}\)GC (tính chất đường trung tuyến của tam giác)
GK = \({1 \over 2}\)GC (gt)
Suy ra: GE = GK
Tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

b. Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK
mà DH = \({1 \over 2}\)BD; EK = \({1 \over 2}\)CE
nên DH = EK ⇒ BD = CE ⇒ ∆ ABC cân tại A
Vậy ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.
c. Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.
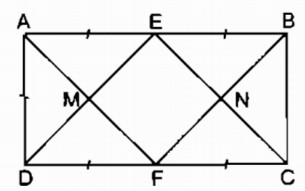
Câu 162: Cho hình bình hành ABCD có AB = 2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD.
a. Các tứ giác AEFD, AECF là hình gì ? Vì sao ?
b. Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
c. Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông ?


a. Xét tứ giác AEFD:
AB // CD (gt) hay AE // FD
AE = \({1 \over 2}\)AB (gt)
FD = \({1 \over 2}\)CD (gt)
Suy ra: AE = FD
Tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
AD = AE = \({1 \over 2}\)AB
Vậy tứ giác AEFD là hình thoi.
Advertisements (Quảng cáo)
Xét tứ giác AECF : AE // CF (gt)
AE = \({1 \over 2}\)AB (gt)
CF = \({1 \over 2}\)CD (gt)
Suy ra: AE = CF
Tứ giác AECF là hình bình hành (vì có một cặp canh đối song song và bằng nhau)
b. Tứ giác AECF là hình thoi
⇒ AF ⊥ ED ⇒ \(\widehat {EMF} = {90^0}\)
AF // CE (vì tứ giác AECF là hình bình hành)
Suy ra: CE ⊥ ED \( \Rightarrow \widehat {MEN} = {90^0}\)
Xét tứ giác EBFD ta có: EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Xét tứ giác EBFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ DE // BF
Suy ra: BF ⊥ AF = 1v
Vậy tứ giác EMFN là hình chữ nhật.
c. Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = \( \Rightarrow \widehat {MEN} = {90^0}\)DE (tính chất hình thoi)
MF = \( \Rightarrow \widehat {MEN} = {90^0}\)AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ \(\widehat A = {90^0}\) ⇒ Hình bình hành ABCD là hình chữ nhật
Ngược lại: ABCD là hình chữ nhật ⇒\(\widehat A = {90^0}\)
Advertisements (Quảng cáo)
Hình thoi AEFD có \(\widehat A = {90^0}\) nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có hai cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2 AD.
Câu 163: Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a. Tứ giác DEBF là hình gì ? Vì sao ?
b. Chứng minh rằng các đường thẳng AC, BD, EF cùng cắt nhau tại một điểm.
c. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.


a. Xét tứ giác DEBF: AB // CD (gt) hay DF // EB
EB = \({1 \over 2}\)AB (gt)
DF = \({1 \over 2}\)CD (gt)
Suy ra: EB = DF
Tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
b. Gọi O là giao điểm của AC và BD
OB = OD (tính chất hình bình hành)
Tứ giác DEBF là hình bình hành
nên EF và BD cắt nhau tại trung điểm của mỗi đường
Suy ra: EF đi qua trung điểm O của BD
Vậy AC, BD và EF cắt nhau tại O trung điểm của mỗi đoạn
c. Xét ∆ EOM và ∆ FON:
\(\widehat {MEO} = \widehat {NFO}\) (so le trong)
OE = OF (tính chất hình bình hành)
\(\widehat {MOE} = \widehat {NOF}\) (đối đỉnh)
Do đó : ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường )
Câu 164: Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD.
a. Tính khoảng cách từ I đến AB
b. Khi điểm M di chuyển trên đoạn thẳng AB thì điểm I di chuyển trên đường nào ?


a. Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
⇒ CE // DF // IH
IC = ID (gt)
nên IH là đường trung bình của hình thang DCEF
\( \Rightarrow IH = {{DF + CE} \over 2}\) (1)
C là tâm hình vuông AMNP
⇒ ∆ CAM là tam giác vuông cân tại C
CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)
⇒ CE = \({1 \over 2}\)AM
D là tâm hình vuông BMLK ⇒ ∆ DBM vuông cân tại D
DF ⊥ BM
⇒ DF là đường trung tuyến (tính chất tam giác cân) ⇒ DF = \({1 \over 2}\)BM
Vậy CE + DF = \({1 \over 2}\)AM + \({1 \over 2}\)BM = \({1 \over 2}\) (AM + BM) = \({1 \over 2}\)AB = \({a \over 2}\) ⇒ IH = \({{{a \over 2}} \over 2} = {a \over 4}\)
b. Gọi Q là giao điểm của BL và AN
Ta có: AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hai góc kề bù)
Suy ra: BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định.
M thay đổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng \({a \over 4}\) nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng \({a \over 4}\)
Khi M trùng B thì I trùng với S là trung điểm của BQ
Khi M trùng với A thì I trùng với R là trung điểm của AQ
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng \({a \over 4}\) .

