Câu 1.1: Mỗi câu sau đây đúng hay ai ?
a. Tam giác và tứ giác không phải là đa giác
b. Hình gồm n đoạn thẳng đôi một có một điểm chung được gọi là đa giác (với n là ố tự nhiên lớn hơn 2)
c. Hình gồm n đoạn thẳng (n là ố tự nhiên lớn hơn 2) trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng được gọi là đa giác.
d. Hình tạo bởi nhiều hình tam giác được gọi là đa giác
e. Đa giác luôn nằm trong nửa mặt phẳng cho trước được gọi là đa giác lồi
f. Đa giác luôn nằm trong nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh của nó được gọi là đa giác lồi
g. Hình gồm hai đa giác lồi cho trước là một đa giác lồi.
a. ai; b. ai; c. Đúng; d. ai; e. ai; f. ai; g. ai
Câu 1.2: a. Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
b. Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
c. Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
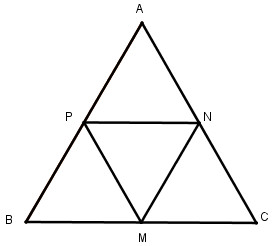
a. Ta có: M là trung điểm của BC
N là trung điểm của AC
nên MN là đường trung bình của ∆ ABC ⇒ MN = \({1 \over 2}\)AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của ∆ ABC
⇒ MP = \({1 \over 2}\)AC
NP là đường trung bình của ∆ ABC ⇒ NP = \({1 \over 2}\)BC
mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy ∆ MNP đều
b.
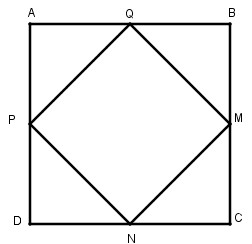
Xét ∆ APQ và ∆ BQM:
AQ = BQ (gt)
\(\widehat A = \widehat B = {90^0}\)
AP = BM (gt)
Do đó: ∆ APQ = ∆ BQM (c.g.c) ⇒ PQ = QM (1)
Xét ∆ BQM và ∆ CMN:
BM = CM (gt)
\(\widehat B = \widehat C = {90^0}\)
BQ = CN (gt)
Do đó: ∆ BQM = ∆ CMN (c.g.c) ⇒ QM = MN (2)
Xét ∆ CMN và ∆ DNP:
CN = DN (gt)
\(\widehat C = \widehat D = {90^0}\)
CM = DP (gt)
Do đó: ∆ CMN = ∆ DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) uy ra: MN = NP = PQ = QM
Advertisements (Quảng cáo)
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên ∆ APQ vuông cân tại A
BQ = BM nên ∆ BMQ vuông cân tại B
\( \Rightarrow \widehat {AQP} = \widehat {BQM} = {45^0}\)
\(\widehat {AQP} + \widehat {PQM} + \widehat {BQM} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {PQM} = {180^0} – \left( {\widehat {AQP} + \widehat {BQM}} \right)\)
\(= {180^0} – \left( {{{45}^0} + {{45}^0}} \right) = {90^0}\)
Vậy tứ giác MNPQ là hình vuông.
c.
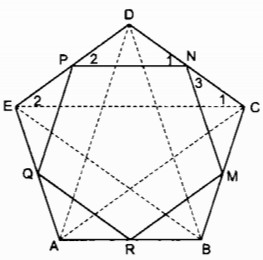
Xét ∆ ABC và ∆ BCD:
AB = BC (gt)
\(\widehat B = \widehat C\) (gt)
BC = CD (gt)
Do đó: ∆ ABC = ∆ BCD (c.g.c)
⇒ AC = BD (1)
Xét ∆ BCD và ∆ CDE:
BC = CD (gt)
\(\widehat C = \widehat D\) (gt)
CD = DE (gt)
Do đó: ∆ BCD = ∆ CDE (c.g.c) ⇒ BD = CE (2)
Xét ∆ CDE và ∆ DEA:
CD = DE (gt)
\(\widehat D = \widehat E\) (gt)
DE = EA (gt)
Do đó: ∆ CDE = ∆ DEA (c.g.c) ⇒ CE = DA (3)
Advertisements (Quảng cáo)
Xét ∆ DEA và ∆ EAB:
DE = EA (gt)
\(\widehat E = \widehat A\) (gt)
EA = AB (gt)
Do đó: ∆ DEA = ∆ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) uy ra: AC = BD = CE = DA = EB
Trong ∆ ABC ta có RM là đường trung bình
⇒ RM = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong ∆ BCD ta có MN là đường trung bình
⇒ MN = \({1 \over 2}\)BD (tính chất đường trung bình của tam giác)
Trong ∆ CDE ta có NP là đường trung bình
⇒ NP = \({1 \over 2}\)CE (tính chất đường trung bình của tam giác)
Trong ∆ 9DEA ta có PQ là đường trung bình
⇒ PQ = \{1 \over 2}\)DA (tính chất đường trung bình của tam giác)
Trong ∆ EAB ta có QR là đường trung bình
⇒ QR = \({1 \over 2}\)EB (tính chất đường trung bình của tam giác)
uy ra: MN = NP = PQ = QR = RM
Ta có: \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = {{\left( {5 – 2} \right){{.180}^0}} \over 5} = {108^0}\)
∆ DPN cân tại D
\( \Rightarrow \widehat {DPN} = \widehat {DNP} = {{{{180}^0} – \widehat D} \over 2} = {{{{180}^0} – {{108}^0}} \over 2} = {36^0}\)
∆ CNM cân tại C
\( \Rightarrow \widehat {CNM} = \widehat {CMN} = {{{{180}^0} – \widehat C} \over 2} = {{{{180}^0} – {{108}^0}} \over 2} = {36^0}\)
\(\widehat {ADN} + \widehat {PNM} + \widehat {CNM} = {180^0}\)
\( \Rightarrow \widehat {PNM} = {180^0} – \left( {\widehat {ADN} + \widehat {CNM}} \right)\)
\(= {180^0} – \left( {{{36}^0} + {{36}^0}} \right) = {108^0}\)
∆ BMR cân tại B
\(\eqalign{ & \Rightarrow \widehat {BMR} = \widehat {BRM} = {{180^\circ – \widehat B} \over 2} = {{180^\circ – 108^\circ } \over 2} = 36^\circ \cr & \widehat {CMN} + \widehat {NMR} + \widehat {BMR} = 180^\circ \cr & \Rightarrow \widehat {NMR} \cr &= 180^\circ – \left( {\widehat {CMN} + \widehat {BMR}} \right) \cr & = 180^\circ – \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
∆ ARQ cân tại A
\(\eqalign{ & \Rightarrow \widehat {ARQ} = \widehat {AQR} = {{180^\circ – \widehat A} \over 2} = {{180^\circ – 108^\circ } \over 2} = 36^\circ \cr & \widehat {BRM} + \widehat {MRQ} + \widehat {ARQ} = 180^\circ \cr & \Rightarrow \widehat {MRQ} = 180^\circ – \left( {\widehat {BRM} + \widehat {ARQ}} \right) \cr & = 180^\circ – \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
∆ QEP cân tại E
\(\eqalign{ & \Rightarrow \widehat {EQP} = \widehat {EPQ} = {{180^\circ – \widehat E} \over 2} = {{180^\circ – 108^\circ } \over 2} = 36^\circ \cr & \widehat {AQR} + \widehat {RQP} + \widehat {EQP} = 180^\circ \cr & \Rightarrow \widehat {RQP} = 180^\circ – \left( {\widehat {AQR} + \widehat {EQP}} \right) \cr & = 180^\circ – \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr & \widehat {EPQ} + \widehat {QPN} + \widehat {DPN} = 180^\circ \cr & \Rightarrow \widehat {QPN} = 180^\circ – \left( {\widehat {EPQ} + \widehat {DPN}} \right) \cr & = 180^\circ – \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
uy ra : \(\widehat {PNM} = \widehat {NMR} = \widehat {MRQ} = \widehat {RQP} = \widehat {QPN}\)
Vậy MNPQR là ngũ giác đều.
Câu 1.3: Cho hình vuông ABCD có AB = 3cm
Trên tia đối của tia BA lấy điểm K ao cho BK = 1cm
Trên tia đối của tia CB lấy điểm L ao cho CL = 1cm
Trên tia đối của tia DC lấy điểm M ao cho MD = 1cm
Trên tia đối của tia AD lấy điểm N ao cho NA = 1cm
Chứng minh KLMN là hình vuông
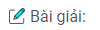
Xét ∆ ANK và ∆ BKL :
AN = BK (gt)
\(\widehat A = \widehat B = 90^\circ \)
AK = BL (vì AB = BC, BK = CL)
Do đó ∆ ANK = ∆ BKL (c.g.c)
⇒ NK = KL (1)
Xét ∆ BKL và ∆ CLM:
BK = CL (gt)
\(\widehat B = \widehat C = 90^\circ \)
BL = CM (vì BC = CD, CL = DM)
Do đó: ∆ BKL = ∆ CLM (c.g.c)
⇒ KL = LM (2)
Xét ∆ CLM và ∆ DMN :
CL = DM (gt)
\(\widehat C = \widehat D = 90^\circ \)
CM = DN (vì CD = DA, DM = AN)
Do đó: ∆ CLM = ∆ DMN (c.g.c)
⇒ LM = MN (3)
Từ (1), (2) và (3) ⇒ NK = KL = LM = MN
Tứ giác MNKL là hình thoi
∆ ANK = ∆ BKL \( \Rightarrow \widehat {ANK} = \widehat {BKL}\)
Trong tam giác ANK có \(\widehat A = 1v \Rightarrow \widehat {ANK} + \widehat {AKN} = 90^\circ \)
\( \Rightarrow \widehat {BKL} + \widehat {AKN} = 90^\circ \)hay \(\widehat {NKL} = 90^\circ \)
Vậy tứ giác MNKL là hình vuông.

