Câu 7.1: Trên đường trung trực của đoạn thẳng AB, lấy hai điểm phân biệt M, N. Khi đó khẳng định nào sau đây đúng?
\(\left( A \right)\widehat {AMN} \ne \widehat {BMN}\)
\(\left( B \right)\widehat {MAN} \ne \widehat {MBN}\)
\(\left( C \right)\widehat {MNA} \ne \widehat {MNB}\)
\(\left( D \right)\Delta AMN = \Delta BMN\)
Vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB. Tương tự, NA = NB. Ta có ∆AMN = ∆BMN (c.c.c) nên các khẳng định (A), (B), (C) sai, (D) đúng.
Câu 7.2: Cho hai tam giác cân chung đáy ABC và ABD, trong đó ABC là tam giác đều. Gọi E là trung điểm của AB. Khi đó, khẳng định nào sau đây là sai?
Advertisements (Quảng cáo)
(A) Đường thẳng CD là đường trung trực của AB.
(B) Điểm E không nằm trên đường thẳng CD.
(C) Đường trung trực của AC đi qua B.
(D) Đường trung trực của BC đi qua A.
Advertisements (Quảng cáo)
Vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB. Tương tự NA = NB. Ta có ∆AMN = ∆BMN (c.c.c) nên các khẳng định (A), (B), (C) sai và (D) đúng.
Đáp số (D) Đường trung trực của BC đi qua A.
Câu 7.3: Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm:
a) AD và CD nếu BD = 5cm; AC = 8cm;
b) AC nếu BD = 11,4cm; AD = 3,2cm.
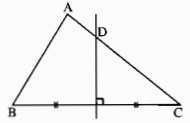
a) Vì D thuộc đường trung trực của BC nên DB = DC. Mặt khác, D ở giữa A và C nên AD = AC – DC
Nếu BD = 5cm; AC = 8cm, thì CD = BD = 5cm và AD = 8 – 5 = 3 (cm).
b) AC = AD + DC = AD + BD = 3,2 + 11,4 = 14,6 (cm).

