
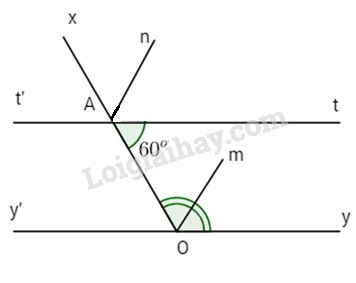
Cho góc \(\widehat {xOy} = {120^o}\). Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là Ox, vẽ tia At sao cho \(\widehat {OAt} = {60^o}\). Gọ At’ là tia đối của tia At.
a) Chứng tỏ tt’ // Oy.
b) Gọi Om, An theo thứ tự là các tia phân giác của các góc \(\widehat {xOy}\) và \(\widehat {xAt}\). Chứng tỏ Om//An.

Advertisements (Quảng cáo)
a) Kẻ Oy’ là tia đối của tia Oy, ta có
\(\widehat {xAn} = \widehat {xOm} = {60^o}\) \(\widehat {xOy} + \widehat {xOy’} = {180^o}\) (kề bù) \( \Rightarrow \widehat {xOy’} = {180^o} – \widehat {xOy’}\)
\( \Rightarrow \widehat {xOy’} = {180^o} – {120^o} = {60^o}.\)
Ta có \( \Rightarrow \widehat {xOy’} = \widehat {OAt} = {60^o}\). Hai góc này ở vị trí so le trong.
Advertisements (Quảng cáo)
Do đó tt’ // Oy.
b) Ta có \(\widehat {xAt} + \widehat {OAt} = {180^o}\)(kề bù)
\( \Rightarrow \widehat {xAt} = {180^o} – \widehat {OAt} \)\(\,= {180^o} – {60^o} = {120^o},\)
Lại có An là tia phân giác của \(\widehat {xAt}\) nên
\(\widehat {xAn} = \widehat {tAn} = \dfrac{1 }{2}\widehat {xAt} = \dfrac{1 }{2}{.120^o} = {60^o}.\)
Tương tự Om là phân giác của \(\widehat {xOy}\) nên
\(\widehat {xOm} = \widehat {yOm} = \dfrac{1 }{ 2}\widehat {xOy} \)\(\,= \dfrac{1}{ 2}{.120^o} = {60^o}.\)
Khi đó \(\widehat {xAn} = \widehat {xOm} = {60^o}\). Hai góc này ở vị trí đồng vị. Do đó Om // An.

