
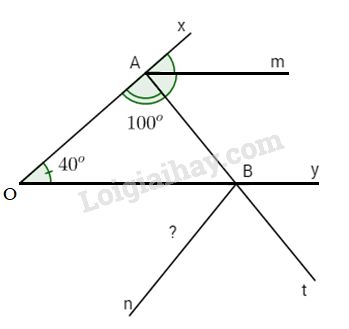
Cho \(\widehat {xOy} = {40^o}\). Lấy A trên tia Ox. Vẽ tia At nằm trên nửa mặt phẳng bờ là đường thẳng Ox. Chứa tia Oy sao cho At cắt Oy tại B và \(\widehat {OAt} = {100^o}\). Gọi Am là tia phân giác của góc \(\widehat {xAt}\).
a) Chứng tỏ Am // Oy.
b) Trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng Oy vẽ tia Bn. Hỏi để Bn song song với Ox thì số đo góc OBn phải bằng bao nhiêu?

Advertisements (Quảng cáo)
a) Ta có \(\widehat {xAt} + \widehat {OAt} = {180^o}\)(kề bù)
Advertisements (Quảng cáo)
\(\eqalign{ & \Rightarrow \widehat {xAt} = {180^o} – \widehat {OAt} \cr & \,\,\,\,\,\widehat {xAt} = {180^o} – {100^o} \cr} \)
\(\widehat {xAt} = {80^o}\)
Am là tia phân giác của \(\widehat {xAt}\) nên
\(\widehat {xAm} = \widehat {tAm} = \dfrac{{\widehat {xAt}}}{ 2} = \dfrac{{{{80}^o}} }{ 2} = {40^0}.\)
Hai góc \(\widehat {xAm}\) và \(\widehat {xOy}\)ở vị trí đồng vị và \(\widehat {xAm} = \widehat {xOy} = {40^o}\). Do đó Am // Oy.
b) Hai góc \(\widehat {OBn}\) và \(\widehat {xOy}\) ở vị trí so le trong để Bn // Ox thì \(\widehat {OBn} = \widehat {xOy} = {40^o}.\)

