
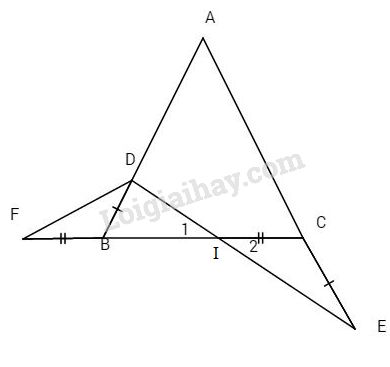
Cho tam giác ABC cân tại A. Trên AB lấy D. Trên tia đối của tia CA. Lấy điểm E sao cho CE = BD, DE cắt BC tại I. Trên tia đối của tia BC lấy F sao cho BF = CI. Chứng minh:
a) \(\Delta BFD = \Delta CIE\)
b) \(\Delta DFI\) cân.
c) I là trung điểm của DE.

Advertisements (Quảng cáo)
a) \(\Delta ABC\) cân tại A \( \Rightarrow \widehat B = \widehat C \)
\(\Rightarrow \widehat {DBF} = \widehat {ECI}\) (1) (cùng bù với \(\widehat B = \widehat C\))
Xét \(\Delta BFD \) và \( \Delta CIE\) có:
+) \(\widehat {DBF} = \widehat {ECI}\)
Advertisements (Quảng cáo)
+) \(BD = CE\) (giả thiết)
+) \(BF = CI\) (giả thiết).
Vậy \(\Delta BFD = \Delta CIE\) (c.g.c).
b) Ta có \(\widehat {{I_1}} = \widehat {{I_2}}\) (đối đỉnh), mà \(\widehat {{I_2}} = \widehat F\) (chứng minh trên) \( \Rightarrow \widehat {{I_1}} = \widehat F\)
Vậy tam giác DFI cân.
c) Tam giác DFI cân (chứng minh trên)
\( \Rightarrow FD = ID\). Lại có \(\Delta BFD = \Delta CIE\) (chứng minh trên)
\( \Rightarrow FD = IE\).
Do đó \(ID = IE\) hay I là trung điểm của DE.

