Bài 3.9: Trong không gian Oxyz cho một vecto \(\overrightarrow a \) tùy ý khác vecto \(\overrightarrow 0 \). Gọi \(\alpha ,\beta ,\gamma \) là ba góc tạo bởi ba vecto đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) trên ba trục Ox, Oy, Oz và vecto \(\overrightarrow a \) . Chứng minh rằng: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
Gọi \(\overrightarrow {{a_0}} \) là vecto đơn vị cùng hướng với vecto \(\overrightarrow a \) , ta có \(\overrightarrow {{a_0}} = {1 \over {|\overrightarrow a |}}\overrightarrow a \).
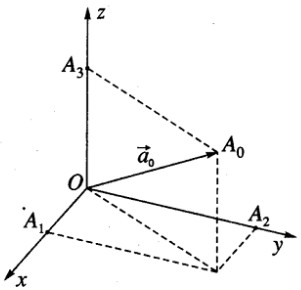
Gọi \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \) và các điểm A1, A2, A3 theo thứ tự là hình chiếu vuông góc của điểm A0 trên các trục Ox, Oy, Oz.
Khi đó ta có: \({{|\overrightarrow {O{A_1}} |} \over {|\overrightarrow {O{A_0}} |}} = \cos \alpha ,{{|\overrightarrow {O{A_2}} |} \over {|\overrightarrow {O{A_0}|} }} = \cos \beta ,{{|\overrightarrow {O{A_3}} |} \over {|\overrightarrow {O{A_0}} |}} = \cos \gamma \)
Vì \(|\overrightarrow {O{A_0}} | = 1\) nên \(|\overrightarrow {O{A_1}} | = \cos \alpha ,|\overrightarrow {O{A_2}} | = \cos \beta ,|\overrightarrow {O{A_3}} | = \cos \gamma \)
Ta có \(\overrightarrow {O{A_0}} = \overrightarrow {O{A_1}} + \overrightarrow {O{B_2}} + \overrightarrow {O{A_3}} \) , ta suy ra: \(\overrightarrow {O{A_0}} = \cos \alpha \overrightarrow i + \cos \beta \overrightarrow j + \cos \gamma \overrightarrow k \) hay \(\overrightarrow {O{A_0}} = (\cos \alpha ;\cos \beta ;\cos \gamma )\) .
Vì \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \) mà \(|\overrightarrow {{a_0}} | = 1\) nên ta có: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
Bài 3.10: Cho hình tứ diện ABCD.
a) Chứng minh hệ thức:
Advertisements (Quảng cáo)
\(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\)
b) Từ hệ thức trên hãy suy ra định lí: “Nếu một hình tứ diện có hai cặp cạnh đối diện vuông góc với nhau thì cặp cạnh đối diện thứ ba cũng vuông góc với nhau.”
a) Ta có: \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} (\overrightarrow {AD} – \overrightarrow {AC} ) = \overrightarrow {AB} .\overrightarrow {AD} – \overrightarrow {AB} .\overrightarrow {AC} \) (1)
\(\overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} (\overrightarrow {AB} – \overrightarrow {AD} ) = \overrightarrow {AC} .\overrightarrow {AB} – \overrightarrow {AC} .\overrightarrow {AD} \) (2)
\(\overrightarrow {AD} .\overrightarrow {BC} = \overrightarrow {AD} (\overrightarrow {AC} – \overrightarrow {AB} ) = \overrightarrow {AD} .\overrightarrow {AC} – \overrightarrow {AD} .\overrightarrow {AB} \) (3)
Lấy (1) + (2) + (3) ta có hệ thức cần chứng minh là:
Advertisements (Quảng cáo)
\(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\)
b) Từ hệ thức trên ta suy ra định lí: “Nếu tứ diện ABCD có \(AB \bot CD,AC \bot DB\) , nghĩa là \(\overrightarrow {AB} .\overrightarrow {CD} = 0\) và \(\overrightarrow {AC} .\overrightarrow {DB} = 0\) thì \(\overrightarrow {AD} .\overrightarrow {BC} = 0\) và do đó \(AD \bot BC\) .”
Bài 3.11: Tính tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \) trong không gian với các tọa độ đã cho là:
a) \(\overrightarrow a = (3;0; – 6),\overrightarrow b = (2; – 4;c)\)
b) \(\overrightarrow a = (1; – 5;2),\overrightarrow b = (4;3; – 5)\)
c) \(\overrightarrow a = (0;\sqrt 2 ;\sqrt 3 ),\overrightarrow b = (1;\sqrt 3 ; – \sqrt 2 )\)

a) \(\overrightarrow a .\overrightarrow b = 6(1 – c)\) ;
b) \(\overrightarrow a .\overrightarrow b = – 21\)
c) \(\overrightarrow a .\overrightarrow b = 0\)
Bài 3.12: Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau:
a) A(4; -1; 1) , B(2; 1; 0)
b) A(2; 3; 4) , B(6; 0; 4)

a) \(|\overrightarrow {AB} | = 3\)
b) \(|\overrightarrow {AB} | = 5\)

