Bài 3.1: Trong không gian Oxyz cho ba vecto \(\overrightarrow a = (2; – 1;2),\overrightarrow b = (3;0;1),\overrightarrow c = ( – 4;1; – 1)\) . Tìm tọa độ của các vecto \(\overrightarrow m \) và \(\overrightarrow n \) biết rằng:
a) \(\overrightarrow m = 3\overrightarrow a – 2\overrightarrow b + \overrightarrow c \)
b)\(\overrightarrow n = 2\overrightarrow a + \overrightarrow b + 4\overrightarrow c \)

\(\overrightarrow m = ( – 4; – 2;3),\overrightarrow n = ( – 9;2;1)\)
Bài 3.2: Trong không gian Oxyz cho vecto \(\overrightarrow a = (1; – 3;4)\).
a) Tìm y0 và z0 để cho vecto \(\overrightarrow b = (2;{y_0};{z_0})\) cùng phương với \(\overrightarrow a \)
b) Tìm tọa độ của vecto \(\overrightarrow c \) biết rằng \(\overrightarrow a \) và \(\overrightarrow c \) ngược hướng và \(|\overrightarrow {c|} = 2|\overrightarrow a |\)
a) Ta biết rằng \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khi và chỉ khi \(\overrightarrow a = k\overrightarrow b \) với k là một số thực. Theo giả thiết ta có: \(\overrightarrow b = ({x_0};{y_0};{z_0})\) với x0 = 2. Ta suy ra \(k = {1 \over 2}\) nghĩa là \(l = {1 \over 2}{x_0}\)
Do đó: \( – 3 = {1 \over 2}{y_0}\) nên y0 = -6
Advertisements (Quảng cáo)
\(4 = {1 \over 2}{z_0}\) nên z0 = 8
Vậy ta có \(\overrightarrow b = (2; – 6;8)\)
b) Theo giả thiết ta có \(\overrightarrow c = – 2\overrightarrow a \)
Do đó tọa độ của \(\overrightarrow c \) là: \(\overrightarrow c \) = (-2; 6; -8).
Bài 3.3: Trong không gian Oxyz cho điểm M có tọa độ (x0; y0 ; z0). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).
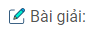
Advertisements (Quảng cáo)
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có: M’(x0; y0; 0)
M’’ (0; y0; z0)
M’’’(x0; 0; z0)
Bài 3.4: Cho hai bộ ba điểm:
a) A = (1; 3; 1) , B = (0; 1; 2) , C = (0; 0; 1)
b) M = (1; 1; 1) , N = (-4; 3; 1) , P = (-9; 5; 1)
Hỏi bộ nào có ba điểm thẳng hàng?
a) Ta có \(\overrightarrow {AB} = ( – 1; – 2;1)\)
\(\overrightarrow {AC} = ( – 1; – 3;0)\)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương, nghĩa là \(\overrightarrow {AB} = k\overrightarrow {AC} \) với k là một số thực.
Giả sử ta có \(\overrightarrow {AB} = k\overrightarrow {AC} \) , khi đó \(\left\{ {\matrix{{k.( – 1) = – 1} \cr {k.( – 3) = – 2}\cr {k.(0) = 1} \cr} } \right.\)
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
b) Ta có: \(\overrightarrow {MN} = ( – 5;2;0)\) và \(\overrightarrow {MP} = ( – 10;4;0)\). Hai vecto \(\overrightarrow {MN} \) và \(\overrightarrow {MP} \) thỏa mãn điều kiện: \(\overrightarrow {MN} = k\overrightarrow {MP} \) với \(k = {1 \over 2}\) nên ba điểm M, N, P thẳng hàng.

