(Đề thi tốt nghiệp THPT năm 2008)
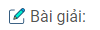
TXĐ: D = R\{0}
\(\eqalign{
& f'(x) = 1 – {9 \over {{x^2}}} = {{{x^2} – 9} \over {{x^2}}} \cr
& f'(x) = 0 < = > x = \pm 3 \cr} \)
Hàm số nghịch biến trong các khoảng (-3; 0), (0; 3) và đồng biến trong các khoảng \(( – \infty ;3),(3; + \infty )\)
Bảng biến thiên:
Ta có: \({\rm{[}}2;4] \subset (0; + \infty );f(2) = 6,5;f(3) = 6;f(4) = 6,25\)
Suy ra : \(\mathop {\min }\limits_{{\rm{[}}2;4]} f(x) = f(3) = 6;\mathop {\max }\limits_{{\rm{[}}2;4]} f(x) = f(2) = 6,5\).
Bài 1.24: Tìm các giá trị của m để phương trình : x3 – 3x2 – m = 0 có ba nghiệm phân biệt.
Advertisements (Quảng cáo)
Đặt f(x) = x3 – 3x2 (C1)
y = m (C2)
Phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt khi và chỉ khi (C1) và (C2) có ba giao điểm.
Ta có: \(\eqalign{
& f'(x) = 3{x^2} – 6x = 3x(x – 2) = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right. \cr} \)
Advertisements (Quảng cáo)
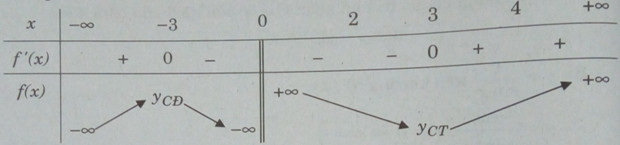
Bảng biến thiên:
Suy ra (C1),(C2) cắt nhau tại 3 điểm khi -4 < m < 0
Kết luận : Phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.
Bài 1.25: Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất.
Cho m > 0. Đặt x là số thứ nhất, 0 < x < m , số thứ hai là m – x
Xét tích P(x) = x(m – x)
Ta có: P’(x) = – 2x + m
\(P'(x) = 0 < = > x = {m \over 2}\)
Bảng biến thiên
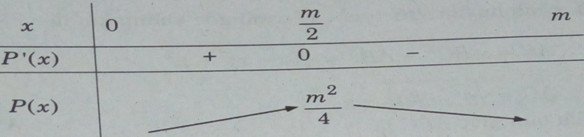
Từ đó ta có giá trị lớn nhất của tích hai số là: \(\mathop {\max }\limits_{(0;m)} P(x) = P({m \over 2}) = {{{m^2}} \over 4}\).
