Bài 26: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là
\(f\left( t \right) = 45{t^2} – {t^3},t = 0,1,2,…,25\)
Nếu coi \(f\) là hàm số xác định trên đoạn \(\left[ {0;25} \right]\) thì \(f’\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\).
a) Tính tốc độ truyền bệnh vào ngày thứ \(5\);
b) Xác định ngày mà tốc độ truyền bệnh là lớn nhất và tính tốc độ đó;
c) Xác định các ngày mà tốc độ truyền bệnh lớn hơn \(600\);
d) Xét chiều biến thiên của hàm số \(f\) trên đoạn \(\left[ {0;25} \right]\).
Giải
Số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 45{t^2} – {t^3}\), \(t\) nguyên và thuộc \(\left[ {0;25} \right]\)
Để xét tốc độ truyền bệnh người ta xem hàm số \(f\) xác định trên đoạn \(\left[ {0;25} \right]\).
a) \(f’\left( t \right) = 90t – 3{t^2} = 3t\left( {30 – t} \right)\)
Tốc độ truyền bệnh vào ngày thứ năm là \(f'(5) = 375\) (người/ngày)
b) \(f”\left( t \right) = 90 – 6t;f”\left( t \right) = 0 \Leftrightarrow t = 15,f’\left( t \right) = 675\)
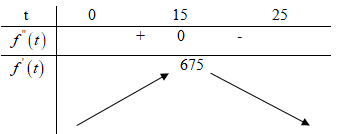
Tốc độ truyền bệnh là lớn nhất vào ngày \(15\).
Tốc độ đó là \(f’\left( {15} \right) = 675\) (người/ngày)
c) \(f’\left( t \right) > 0 \Leftrightarrow 90t – 3{t^2} > 600\)
\(\Leftrightarrow {t^2} – 30t + 200 < 0 \Leftrightarrow 10 < t < 20\)
Advertisements (Quảng cáo)
Từ ngày thứ \(11\) đến ngày thứ \(19\), tốc độ truyền bệnh là lớn hơn \(600\) người mỗi ngày.
Bài 27: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(f\left( x \right) = \sqrt {3 – 2x} \) trên đoạn \(\left[ { – 3;1} \right]\);
b) \(f\left( x \right) = x + \sqrt {4 – {x^2}} \)
c) \(f\left( x \right) = {\sin ^4}x + {\cos ^2}x + 2;\)
d) \(f\left( x \right) = x – \sin 2x\) trên đoan \(\left[ { – {\pi \over 2};\pi } \right]\).
Giải
a) TXĐ: \(D = \left[ { – 3;1} \right]\); \(f’\left( x \right) = {{ – 1} \over {\sqrt {3 – 2x\,} }} < 0\) với mọi \(x < {3 \over 2}\,\)
Hàm số \(f\) nghịch biến trên đoạn \(\left[ { – 3;1} \right]\)
Do đó \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { – 3;1} \right]} = f\left( { – 3} \right) = 3\); \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { – 3;1} \right]} = f\left( 1 \right) = 1\)
b) TXĐ: \(D = \left[ { – 2;2} \right];f’\left( x \right) = 1 – {x \over {4 – {x^2}}}\) với \(x \in \left( { – 2;2} \right)\)
Advertisements (Quảng cáo)
\(f’\left( x \right) = 0 \Leftrightarrow 1 – {x \over {4 – {x^2}}} = 0 \Leftrightarrow \sqrt {4 – {x^2}} = x \)
\(\Leftrightarrow \left\{ \matrix{
0 < x < 2 \hfill \cr
4 – {x^2} = {x^2} \hfill \cr} \right. \Leftrightarrow x = \sqrt 2 \)
Ta có \(f\left( { – 2} \right) = – 2;f\left( {\sqrt 2 } \right) = 2\sqrt 2 ;f\left( 2 \right) = 2\)
Vậy \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { – 2;2} \right]} = 2\sqrt 2 ;\,\,\,\mathop {\min f\left( x \right)}\limits_{x \in \left[ { – 2;2} \right]} = – 2\)
c) TXĐ: \(D =\mathbb R\)
Ta có: \(f\left( x \right) = {\sin ^4}x + 1 – {\sin ^2}x + 2 = {\sin ^4}x – {\sin ^2}x + 3\)
Đặt \(t = {\sin ^2}x;0 \le t \le 1\)
Tìm giá trị nhỏ nhất, lớn nhất của hàm \(g\left( t \right) = {t^2} – t + 3\) số trên đoạn \(\left[ {0;1} \right]\)
\(g’\left( t \right) = 2t – 1;g’\left( t \right) = 0 \Leftrightarrow t = {1 \over 2}\)
Ta có: \(g\left( 0 \right) = 3;g\left( {{1 \over 2}} \right) = {{11} \over {14}};g\left( 1 \right) = 3\)
Do đó: \(\mathop {\min g\left( t \right)}\limits_{t \in \left[ {0;1} \right]} = {{11} \over {14}};\,\,\,\,\,\,\mathop {\max g\left( t \right)}\limits_{t \in \left[ {0;1} \right]} = 3\)
Vậy: \(\mathop {\min f\left( x \right)}\limits_{x \in {\mathbb{R}}} = {{11} \over {14}};\,\,\,\,\,\,\mathop {\max f\left( x \right)}\limits_{x \in {\mathbb{R}}} = 3\)
d) TXĐ: \(D = \left[ { – {\pi \over 2};\pi } \right]\)
\(f’\left( x \right) = 1 – 2\cos 2x;\)
\(f’\left( x \right) = 0 \Leftrightarrow \cos 2x = {1 \over 2} = \cos {\pi \over 3}\)
\(\Leftrightarrow 2x = \pm {\pi \over 3} + k2\pi \Leftrightarrow x = \pm {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}\)
Với \( – {\pi \over 2} < x < \pi ,f’\left( x \right) = 0\) tại các điểm \( – {\pi \over 6},{\pi \over 6}\) và \({{5\pi } \over 6}\)
Ta có \(f\left( { – {\pi \over 6}} \right) = – {\pi \over 6} + {{\sqrt 3 } \over 2};f\left( {{\pi \over 6}} \right) = {\pi \over 6} – {{\sqrt 3 } \over 2};\)
\(f\left( {{{5\pi } \over 6}} \right) = {{5\pi } \over 6} + {{\sqrt 3 } \over 2}\);
.\(f\left( { – {\pi \over 2}} \right) = – {\pi \over 2};f\left( \pi \right) = \pi \)
So sánh năm giá trị trên ta được:
\(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { – {\pi \over 2};\pi } \right]} = {{5\pi } \over 6} + {{\sqrt 3 } \over 2}\) và \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { – {\pi \over 2};\pi } \right]} = – {\pi \over 2}\)
Bài 28: Trong các hình chữ nhật có chu vi là \(40cm\), hãy xác định hình chữ nhật có diện tích lớn nhất.
Giải
Gọi \(x (cm)\) là độ dài một cạnh của hình chữ nhật thì cạnh kia có độ dài \(20 – x (cm)\).
Điều kiện: \(0<x<20\)
Diện tích hình chữ nhật là \(S\left( x \right) = x\left( {20 – x} \right) = 20x – {x^2}\) với \(x \in \left( {0;20} \right)\)
Ta có \(S’\left( x \right) = 20 – 2x;S’\left( x \right) = 0 \Leftrightarrow x = 10\)
\(S\left( {10} \right) = 100\)
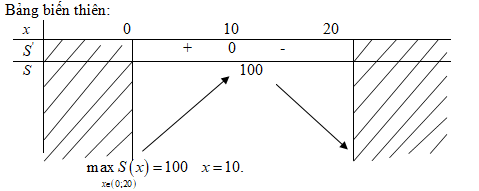
Vậy hình chữ nhật có diện tích lớn nhất khi nó là hình vuông có cạnh dài \(10 cm\).

