Bài 1.20: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = -3x2 + 4x – 8 trên đoạn [0; 1]
b) f(x) = x3 + 3x2 – 9x – 7 trên đoạn [-4; 3]
c) \(f(x) = \sqrt {25 – {x^2}} \) trên đoạn [-4; 4]
d) f(x) = |x2 – 3x + 2| trên đoạn [-10; 10]
e) \(f(x) = {1 \over {\sin x}}\) trên đoạn \({\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}\)
g) \(f(x) = 2\sin x + \sin 2x\) trên đoạn \({\rm{[}}0;{{3\pi } \over 2}{\rm{]}}\)
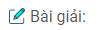
a) f(x) = -3x2 + 4x – 8 trên đoạn [0; 1]
\(\eqalign{
& f'(x) = – 6x + 4,f'(x) = 0 < = > x = {2 \over 3} \cr
& f({2 \over 3}) = – {{20} \over 3},f(0) = – 8;f(1) = – 7 \cr} \)
Vậy \(\mathop {\min }\limits_{{\rm{[}}0;1]} f(x) = – 8;\mathop {\max }\limits_{{\rm{[}}0;1]} f(x) = – {{20} \over 3}\)
b) f(x) = x3 + 3x2 – 9x – 7 trên đoạn [-4; 3]
\(f'(x) = 3{x^2} + 6x – 9\)
\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = – 3 \hfill \cr} \right.\)
Hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = 1 và fCĐ = f(-3) = 20; fCT = f(1) = -12 ;
f(-4) = 13 ; f(3) = 20.
Vậy \(\mathop {\min }\limits_{{\rm{[}} – 4;3]} f(x) = – 12;\mathop {\max }\limits_{{\rm{[}} – 4;3]} f(x) = 20\)
c) \(f(x) = \sqrt {25 – {x^2}} \) trên đoạn [-4; 4]
\(f'(x) = {{ – x} \over {\sqrt {25 – {x^2}} }};f'(x) > 0\) trên khoảng (-4; 0) và
f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và fCĐ = 5
Advertisements (Quảng cáo)
Mặt khác, ta có f(-4) = f(4) = 3
Vậy \(\mathop {\min }\limits_{{\rm{[}} – 4;4]} f(x) = 3;\mathop {\max }\limits_{{\rm{[}} – 4;4]} f(x) = 5\)
d) \(f(x) = |{x^2} – 3x + 2|\) trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x2 – 3x + 2.
Ta có:
\(g'(x) = 2x – 3;g'(x) = 0 < = > x = {3 \over 2}\)
Bảng biến thiên:
Vì: \(f(x) = \left\{ \matrix{
g(x),{x^2} – 3x + 2 \ge 0 \hfill \cr
– g(x),{x^2} – 3x + 2 < 0 \hfill \cr} \right.\)
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: \(\mathop {\min }\limits_{{\rm{[}} – 10;10]} f(x) = f(1) = f(2) = 0;\mathop {\max }\limits_{{\rm{[}} – 10;10]} f(x) = f( – 10) = 132\)
e) \(f(x) = {1 \over {\sin x}}\) trên đoạn \({\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}\)
\(f'(x) = – {{\cos x} \over {{{\sin }^2}x}},f'(x) < 0\) nên và f’(x) > 0 trên \(({\pi \over 2};{{5\pi } \over 6}{\rm{]}}\) nên hàm số đạt cực tiểu tại \(x = {\pi \over 2}\) và \({f_{CT}} = f({\pi \over 2}) = 1\)
Mặt khác, \(f({\pi \over 3}) = {2 \over {\sqrt 3 }},f({{5\pi } \over 6}) = 2\)
Vậy \(\mathop {\min }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 1;\mathop {\max }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 2\)
g) \(f(x) = 2\sin x + \sin 2x\) trên đoạn \({\rm{[}}0;{{3\pi } \over 2}{\rm{]}}\)
Advertisements (Quảng cáo)
\(f'(x) = 2\cos x + 2\cos 2x = 4\cos {x \over 2}\cos {{3x} \over 2}\)
\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
\cos {x \over 2} = 0 \hfill \cr
\cos {{3x} \over 2} = 0 \hfill \cr} \right. \Rightarrow \left[ \matrix{
x = \pi \hfill \cr
x = {\pi \over 3} \hfill \cr} \right.\)
Ta có: \(f(0) = 0,f({\pi \over 3}) = {{3\sqrt 3 } \over 2},f(\pi ) = 0,f({{3\pi } \over 2}) = – 2\)
Từ đó ta có : \(\mathop {\min }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = – 2;\mathop {\max }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = {{3\sqrt 3 } \over 2}\).
Bài 1.21: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x \over {4 + {x^2}}}\) trên khoảng \(( – \infty ; + \infty )\) ;
b) \(y = {1 \over {\cos x}}\) trên khoảng \(({\pi \over 2};{{3\pi } \over 2})\)
c) \(y = {1 \over {1 + {x^4}}}\) trên khoảng \(( – \infty ; + \infty )\) ;
d) \(y = {1 \over {\sin x}}\) trên khoảng \((0;\pi )\) .
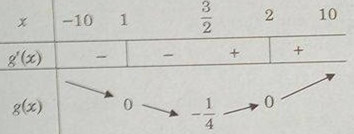
a) \(y = {x \over {4 + {x^2}}}\) trên khoảng \(( – \infty ; + \infty )\)
\(\eqalign{
& y’ = {{4 – {x^2}} \over {{{(4 + {x^2})}^2}}} \cr
& y’ = 0 \Rightarrow \left[ \matrix{
x = – 2 \hfill \cr
x = 2 \hfill \cr} \right. \cr} \)
Từ đó ta có \(\mathop {\min }\limits_R f(x) = – {1 \over 4};\mathop {\max }\limits_R f(x) = {1 \over 4}\)
b) \(y = {1 \over {\cos x}}\) trên khoảng \(({\pi \over 2};{{3\pi } \over 2})\)
\(y’ = {{\sin x} \over {{{\cos }^2}x}};y’ = 0 < = > x = \pi\)
Bảng biến thiên:
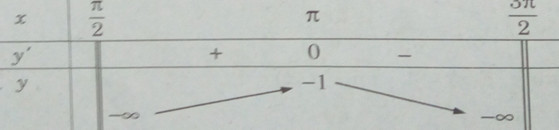
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: \(\mathop {\max }\limits_{({\pi \over 2};{{3\pi } \over 2})} y = y(\pi ) = – 1\)
c) \(y = {1 \over {1 + {x^4}}}\) trên khoảng \(( – \infty ; + \infty )\) ;
\(y’ = {{ – 4{x^3}} \over {{{(1 + {x^4})}^2}}};y’ = 0 < = > x = 0\)
Bảng biến thiên: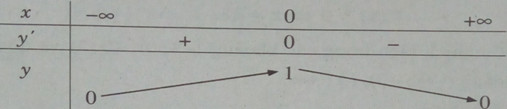 
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất là: \(\mathop {\max }\limits_R y = y(0) = 1\)
d) \(y = {1 \over {\sin x}}\) trên khoảng \((0;\pi )\)
\(y’ = {{ – \cos x} \over {{{\sin }^2}x}},y’ = 0 < = > x = {\pi \over 2}\)
Bảng biến thiên: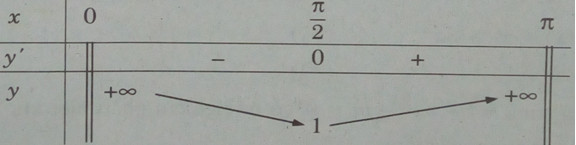
Hàm số không có giá trị lớn nhất. Giá trị nhỏ nhất của hàm số là: \(\mathop {\min }\limits_{(0;\pi )} y = y({\pi \over 2}) = 1\).
Bài 1.22: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = {{2x – 1} \over {x – 3}}\) trên đoạn [0; 2].
(Đề thi tốt nghiệp THPT năm 2008, lần 2)
TXĐ: D =R\{3}
\(f'(x) = – {5 \over {{{(x – 3)}^2}}} < 0,\forall x \in D\) và do đó f(x) nghịch biến trên các khoảng \(( – \infty ;3),(3; + \infty )\)
Ta thấy \({\rm{[}}0;2] \subset ( – \infty ;3).\)
Vì vậy: \(\mathop {\min }\limits_{{\rm{[}}0;2]} f(x) = f(2) = – 3;\mathop {\max }\limits_{{\rm{[}}0;2]} f(x) = f(0) = {1 \over 3}\).
