Bài 23: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức: \(G\left( x \right) = 0,025{x^2}\left( {30 – x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân ( \(x\) được tính bằng miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất và tính độ giảm đó.
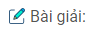
\(D = \left( {0; + \infty } \right)\);
\(G\left( x \right) = 0,75{x^2} – 0,025{x^3}\)
\(G’\left( x \right) = 1,5x – 0,075{x^2};G’\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 20\).
\(\eqalign{
& \mathop {\max G\left( x \right)}\limits_{x > 0} = G\left( {20} \right) = 100 \cr
& \cr} \)
Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là \(20\) mg. Khi đó, độ giảm huyết áp là \(100\).
Bài 24: Cho parabol \((P): y = x^2\) và điểm \(A (-3;0)\). Xác định điểm \(M\) thuộc parabol \((P)\) sao cho khoảng cách \(AM\) là ngắn nhất và tìm khoảng cách ngắn nhất đó.
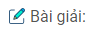
Advertisements (Quảng cáo)
Gọi \(M\left( {x;{x^2}} \right)\)
Ta có: \(A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\)
\(AM\) đạt giá trị nhỏ nhất khi và chỉ khi \(f(x) = {x^4} + {x^2} + 6x + 9\) đạt giá trị nhỏ nhất
Ta có: \(f'(x) = 4{x^3} + 2x + 6 = 2(x + 1)(2{x^2} – 2x + 3)\)
\(f’\left( x \right) = 0 \Leftrightarrow x = – 1;f\left( { – 1} \right) = 5\)
Advertisements (Quảng cáo)
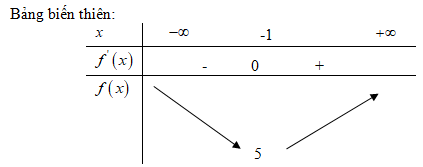
\(f\) đạt giá trị nhỏ nhất tại điểm \(x = -1\), giá trị nhỏ nhất là \(f (-1) = 5\).
\(AM\) đạt giá trị nhỏ nhất khi \(M\) ở vị trí \({M_0} (-1; 1)\) khi đó \(AM_0=\sqrt 5\)
Bài 25: Một con cá hồi bơi ngược dòng để vượt một khoảng cách là \(300km\). Vận tốc dòng nước là \(6 km/h\). Nếu vận tốc bơi của con cá khi nước đứng yên là \(v (km/h)\) thì năng lượng tiêu hao của con cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\), trong đó \(c\) là một hằng số, \(E\) được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Vận tốc của cá hồi khi bơi ngược là \(v – 6 (km/h)\). Thời gian cá bơi để vượt khoảng cách \(300 km\) là: \(t = {{300} \over {v- 6}}\,\,\left( h \right)\)
Năng lượng tiêu hao của cá để vượt khoảng cách đó là:\(E\left( v \right) = c{v^3}.{{300} \over {v – 6}} = 300c.{{{v^3}} \over {v – 6}}\) (jun) với \(v>6\).
Đạo hàm \(E’\left( v \right) = 300c.{{3{v^2}\left( {v – 6} \right) – {v^3}} \over {{{\left( {v – 6} \right)}^2}}} = 300c.{{2{v^3} – 18v} \over {{{\left( {v – 6} \right)}^2}}}\)
\(= 600c.{{{v^2}\left( {v – 9} \right)} \over {{{\left( {v – 6} \right)}^2}}}\)
Năng lượng cực tiểu khi: \(E’\left( v \right) = 0 \Leftrightarrow v = 9\)( vì \(v>6)\)
\(E\left( 9 \right) = 72900c\)
Bảng biến thiên:
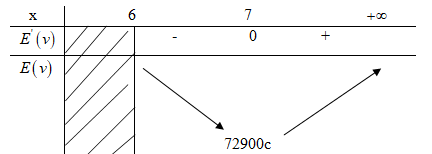
Để ít tiêu hao năng lượng nhất, cá phải bơi với vận tốc ( khi nước đứng yên) là \(9 (km/h)\).

