Bài 3.1: Cho hàm số \(f\left( x \right) = {{\left( {x – 1} \right)\left| x \right|} \over x}\)
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó.
a)
\(f\left( x \right) = {{\left( {x – 1} \right)\left| x \right|} \over x} = \left\{ \matrix{
x – 1,\,{\rm{ nếu }}\,\,x > 0 \hfill \cr
1 – x,\,{\rm{ nếu\,\, x < 0}} \hfill \cr} \right.\) Hàm số này có tập xác định là \(R\backslash \left\{ 0 \right\}\)
b)
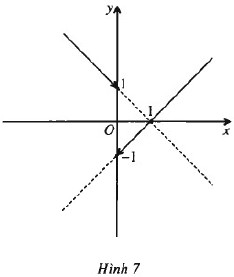
Từ đồ thị (H.7) dự đoán \(f\left( x \right)\) liên tục trên các khoảng \(\left( { – \infty {\rm{ }};{\rm{ }}0} \right),\;\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\) nhưng không liên tục trên R. Thật vậy,
– Với \(x > 0,f\left( x \right) = x – 1\) là hàm đa thức nên liên tục trên R do đó liên tục trên \(\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\)
– Với \(x < 0,f\left( x \right) = 1 – x\) cũng làhàmđa thức nên liên tục trên R do đó liên tục trên \(\left( { – \infty {\rm{ }};{\rm{ }}0} \right)\)
Dễ thấy hàm số gián đoạn tại x = 0 vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = – 1,{\rm{ }}\mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = 1\)
Bài 3.2: Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b; c) nhưng không liên tục trên (a; c)
Advertisements (Quảng cáo)
Xét hàm số
\(f\left( x \right) = \left\{ \matrix{
x + 2,\,{\rm{nếu}} \le {\rm{0}} \hfill \cr
{1 \over {{x^2}}}{\rm\,{,nếu }}\,\,x > 0 \hfill \cr} \right.\)
– Trường hợp \(x \le 0\)
\(f\left( x \right) = x + 2\) là hàmđa thức, liên tục trên R nên nó liên tục trên (-2; 0]
– Trường hợp x > 0
Advertisements (Quảng cáo)
\(f\left( x \right) = {1 \over {{x^2}}}\) là hàm số phân thức hữu tỉ nên liên tục trên (2; 0) thuộc tập xác định của nó.
Như vậy \(f\left( x \right)\) liên tục trên (-2; 0] và trên (0; 2)
Tuy nhiên, vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {1 \over {{x^2}}} = + \infty \) nên hàm số \(f\left( x \right)\) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)
Bài 3.3: Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c)
Vì hàm số liên tục trên (a; b] nên liên tục trên (a; b) và \(\mathop {\lim }\limits_{x \to {b^ – }} f\left( x \right) = f\left( b \right)\) (1)
Vì hàm số liên tục trên [b; c) nên liên tục trên (b; c) và \(\mathop {\lim }\limits_{x \to {b^ + }} f\left( x \right) = f\left( b \right)\) (2)
Từ (1) và (2) suy ra \(f\left( x \right)\) liên tục trên các khoảng (a; b), (b; c) và liên tục tại x = b (vì \(\mathop {\lim }\limits_{x \to b} f\left( x \right) = f\left( b \right)\) ). Nghĩa là nó liên tục trên (a; c)
Bài 3.4: Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) chứa điểm x0
Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} {{f\left( x \right) – f\left( {{x_0}} \right)} \over {x – {x_0}}} = L\) thì hàm số \(f\left( x \right)\) liên tục tại điểm x0
Đặt \(g\left( x \right) = {{f\left( x \right) – f\left( {{x_0}} \right)} \over {x – {x_0}}} – L\) và biểu diễn \(f\left( x \right)\) qua \(g\left( x \right)\)
Đặt \(g\left( x \right) = {{f\left( x \right) – f\left( {{x_0}} \right)} \over {x – {x_0}}} – L\)
Suy ra \(g\left( x \right)\) xác định trên \(\left( {a{\rm{ }};{\rm{ }}b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\)
Mặt khác, \(f\left( x \right) = f\left( {{x_0}} \right) + L\left( {x – {x_0}} \right) + \left( {x – {x_0}} \right)g\left( x \right)\) nên
\(\eqalign{
& \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( {{x_0}} \right) + L\left( {x – {x_0}} \right) + \left( {x – {x_0}} \right)g\left( x \right)} \right] \cr
& = \mathop {\lim }\limits_{x \to {x_0}} f\left( {{x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} L\left( {x – {x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} \left( {x – {x_0}} \right).\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = f\left( {{x_0}} \right). \cr} \)
Vậy hàm số \(y = f\left( x \right)\) liên tục.
