Bài 3.12: Chứng minh phương trình
\({x^n} + {a_1}{x^{n – 1}} + {a_2}{x^{n – 2}} + … + {a_{n – 1}}x + {a_n} = 0\) luôn có nghiệm với n là số tự nhiên lẻ.
Hàm số \(f\left( x \right) = {x^n} + {a_1}{x^{n – 1}} + {a_2}{x^{n – 2}} + … + {a_{n – 1}}x + {a_n}\) xác định trên R
– Ta có \(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^n} + {a_1}{x^{n – 1}} + {a_2}{x^{n – 2}} + … + {a_{n – 1}}x + {a_n}} \right) \cr
& {\rm{ = }}\mathop {\lim }\limits_{x \to + \infty } {x^n}\left( {1 + {{{a_1}} \over x} + {{{a_2}} \over {{x^2}}} + … + {{{a_{n – 1}}} \over {{x^{n – 1}}}} + {{{a_n}} \over {{x^n}}}} \right) = + \infty \cr} \)
Vì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) nên với dãy số \(\left( {{x_n}} \right)\) bất kì mà \({x_n} \to + \infty \) ta luôn có \(\lim f\left( {{x_n}} \right) = + \infty \)
Do đó, \(f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \(f\left( {{x_n}} \right) > 1\) kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại số a sao cho \(f\left( a \right) > 1\) (1)
Advertisements (Quảng cáo)
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to – \infty } \left( {{x^n} + {a_1}{x^{n – 1}} + {a_2}{x^{n – 2}} + … + {a_{n – 1}}x + {a_n}} \right) \cr
& {\rm{ = }}\mathop {\lim }\limits_{x \to – \infty } {x^n}\left( {1 + {{{a_1}} \over x} + {{{a_2}} \over {{x^2}}} + … + {{{a_{n – 1}}} \over {{x^{n – 1}}}} + {{{a_n}} \over {{x^n}}}} \right) = – \infty \cr} \) (do n lẻ).
Vì \(\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = – \infty\) nên với dãy số \(\left( {{x_n}} \right)\) bất kì mà \({x_n} \to – \infty \) ta luôn có \(\lim f\left( {{x_n}} \right) = – \infty \) hay \(\lim \left[ { – f\left( {{x_n}} \right)} \right] = + \infty \)
Do đó, \( – f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \( – f\left( {{x_n}} \right) > 1\) kể từ số hạng nào đó trở đi. Nói cách khác, luôn tồn tại b sao cho \( – f\left( b \right) > 1\) hay \(f\left( b \right) < – 1\) (2)
– Từ (1) và (2) suy ra \(f\left( a \right)f\left( b \right) < 0\)
Mặt khác, \(f\left( x \right)\) hàm đa thức liên tục trên R nên liên tục trên [a; b]
Advertisements (Quảng cáo)
Do đó, phương trình \(f\left( x \right) = 0\) luôn có nghiệm.
Bài 3.13: Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn [a; b]. Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm hay không trong khoảng (a; b)? Cho ví dụ minh hoạ.
Nếu hàm số \(y = f\left( x \right)\) liên tục trên đoạn [a; b] và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
– \(f\left( x \right) = {x^2} – 1\) liên tục trên đoạn \(\left[ { – 2;2} \right],f\left( { – 2} \right)f\left( 2 \right) = 9 > 0\)
Phương trình \({x^2} – 1 = 0\) có nghiệm \(x = \pm 1\) trong khoảng (-2; 2)
– \(f\left( x \right) = {x^2} + 1\) liên tục trên đoạn [-1; 1] và \(f\left( { – 1} \right)f\left( 1 \right) = 4 > 0\). Còn phương trình \({x^2} + 1 = 0\) lại vô nghiệm trong khoảng (-1; 1)
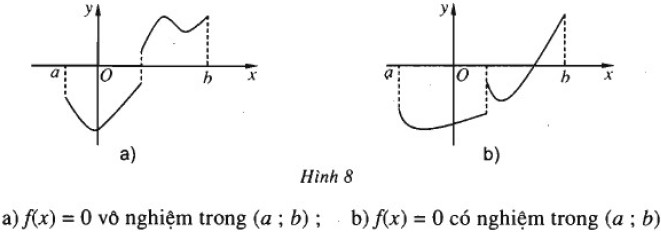
Bài 3.14: Nếu hàm số \(y = f\left( x \right)\) không liên tục trên đoạn [a; b] nhưng \(f\left( a \right)f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm hay không trong khoảng (a; b) ? Hãy giải thích câu trả lời bằng minh hoạ hình học.
Nếu hàm số \(y = f\left( x \right)\) không liên tục trên đoạn [a; b] nhưng \(f\left( a \right)f\left( b \right) < 0\ thì phương trình \(f\left( x \right) = 0\) có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Minh hoạ hình hoạ (H.8):