Bài 2.5: Tìm giới hạn của các hàm số sau :
a) \(f\left( x \right) = {{{x^2} – 2x – 3} \over {x – 1}}\) khi \(x \to 3\) ;
b) \(h\left( x \right) = {{2{x^3} + 15} \over {{{\left( {x + 2} \right)}^2}}}\) khi \(x \to – 2\) ;
c) \(k\left( x \right) = \sqrt {4{x^2} – x + 1} \) khi \(x \to – \infty \) ;
d) \(f\left( x \right) = {x^3} + {x^2} + 1\) khi \(x \to – \infty \) ;
e) \(h\left( x \right) = {{x – 15} \over {x + 2}}\) khi \(x \to – {2^ + }\) và khi \(x \to – {2^ – }\)
Giải :
a) 0 ; b) \( – \infty \) ;
c)
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } \sqrt {4{x^2} – x + 1} \cr
& = \mathop {\lim }\limits_{x \to – \infty } \left| x \right|\sqrt {4 – {1 \over x} + {1 \over {{x^2}}}} \cr
& = \mathop {\lim }\limits_{x \to – \infty } \left( { – x\sqrt {4 – {1 \over x} + {1 \over {{x^2}}}} } \right) = + \infty \cr} \)
d) \(\mathop {\lim }\limits_{x \to – \infty } \left( {{x^3} + {x^2} + 1} \right) = \mathop {\lim }\limits_{x \to – \infty } {x^3}\left( {1 + {1 \over x} + {1 \over {{x^3}}}} \right) = – \infty \)
e) \( – \infty \) và \( + \infty \)
Bài 2.6: Tính các giới hạn sau :
a) \(\mathop {\lim }\limits_{x \to – 3} {{x + 3} \over {{x^2} + 2x – 3}}\) ; b) \(\mathop {\lim }\limits_{x \to 0} {{{{\left( {1 + x} \right)}^3} – 1} \over x}\) ;
c) \(\mathop {\lim }\limits_{x \to + \infty } {{x – 1} \over {{x^2} – 1}}\) ; d) \(\mathop {\lim }\limits_{x \to 5} {{x – 5} \over {\sqrt x – \sqrt 5 }}\) ;
e) \(\mathop {\lim }\limits_{x \to + \infty } = {{x – 5} \over {\sqrt x + \sqrt 5 }}\) ; f) \(\mathop {\lim }\limits_{x \to – 2} {{\sqrt {{x^2} + 5} – 3} \over {x + 2}}\) ;
g) \(\mathop {\lim }\limits_{x \to 1} {{\sqrt x – 1} \over {\sqrt {x + 3} – 2}}\) ; h) \(\mathop {\lim }\limits_{x \to + \infty } {{1 – 2x + 3{x^3}} \over {{x^3} – 9}}\) ;
i) \(\mathop {\lim }\limits_{x \to 0} {1 \over {{x^2}}}\left( {{1 \over {{x^2} + 1}} – 1} \right)\) ; j) \(\mathop {\lim }\limits_{x \to – \infty } {{\left( {{x^2} – 1} \right){{\left( {1 – 2x} \right)}^5}} \over {{x^7} + x + 3}}\) ;
a) \(\mathop {\lim }\limits_{x \to – 3} {{x + 3} \over {{x^2} + 2x – 3}} = \mathop {\lim }\limits_{x \to – 3} {{x + 3} \over {\left( {x – 1} \right)\left( {x + 3} \right)}} = \mathop {\lim }\limits_{x \to – 3} {1 \over {x – 1}} = {{ – 1} \over 4}\)
b) \(\eqalign{
& \mathop {\lim }\limits_{x \to 0} {{{{\left( {1 + x} \right)}^3} – 1} \over x} \cr
& = \mathop {\lim }\limits_{x \to 0} {{\left( {1 + x – 1} \right)\left[ {{{\left( {1 + x} \right)}^2} + \left( {1 + x} \right) + 1} \right]} \over x} \cr
& = \mathop {\lim }\limits_{x \to 0} {{x\left[ {{{\left( {1 + x} \right)}^2} + \left( {1 + x} \right) + 1} \right]} \over x} \cr
& = \mathop {\lim }\limits_{x \to 0} \left[ {{{\left( {1 + x} \right)}^2} + \left( {1 + x} \right) + 1} \right] = 3 \cr} \)
Advertisements (Quảng cáo)
c) \(\mathop {\lim }\limits_{x \to + \infty } {{x – 1} \over {{x^2} – 1}} = \mathop {\lim }\limits_{x \to + \infty } {{{1 \over x} – {1 \over {{x^2}}}} \over {1 – {1 \over {{x^2}}}}} = 0\)
d) \(\mathop {\lim }\limits_{x \to 5} {{x – 5} \over {\sqrt x – \sqrt 5 }}\)
\(= \mathop {\lim }\limits_{x \to 5} {{\left( {\sqrt x – \sqrt 5 } \right)\left( {\sqrt x + \sqrt 5 } \right)} \over {\sqrt x – \sqrt 5 }}\)
\(= \mathop {\lim }\limits_{x \to 5} \left( {\sqrt x + \sqrt 5 } \right) = 2\sqrt 5 \)
e) \(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } {{x – 5} \over {\sqrt x + \sqrt 5 }} \cr
& = \mathop {\lim }\limits_{x \to + \infty } {{1 – {5 \over x}} \over {{1 \over {\sqrt x }} + {{\sqrt 5 } \over x}}} = + \infty \cr} \)
(Vì \({1 \over {\sqrt x }} + {{\sqrt 5 } \over x} > 0\) với mọi \(x > 0\) ).
f) \(\eqalign{
& \mathop {\lim }\limits_{x \to – 2} {{\sqrt {{x^2} + 5} – 3} \over {x + 2}} \cr
& = \mathop {\lim }\limits_{x \to – 2} {{{x^2} + 5 – 9} \over {\left( {x + 2} \right)\left( {\sqrt {{x^2} + 5} + 3} \right)}} \cr
& = \mathop {\lim }\limits_{x \to – 2} {{\left( {x – 2} \right)\left( {x + 2} \right)} \over {\left( {x + 2} \right)\left( {\sqrt {{x^2} + 5} + 3} \right)}} \cr
& = \mathop {\lim }\limits_{x \to – 2} {{x – 2} \over {\sqrt {{x^2} + 5} + 3}} = {{ – 2} \over 3} \cr} \)
g) \(\eqalign{
& \mathop {\lim }\limits_{x \to 1} {{\sqrt x – 1} \over {\sqrt {x + 3} – 2}} \cr
& = \mathop {\lim }\limits_{x \to 1} {{\left( {\sqrt x – 1} \right)\left( {\sqrt {x + 3} + 2} \right)} \over {x + 3 – 4}} \cr
& = \mathop {\lim }\limits_{x \to 1} {{\left( {\sqrt {x – 1} } \right)\left( {\sqrt {x + 3} + 2} \right)} \over {x – 1}} \cr
& = \mathop {\lim }\limits_{x \to 1} {{\left( {\sqrt x – 1} \right)\left( {\sqrt {x + 3} + 2} \right)} \over {\left( {\sqrt x – 1} \right)\left( {\sqrt x + 1} \right)}} \cr
& = \mathop {\lim }\limits_{x \to 1} {{\sqrt {x + 3} + 2} \over {\sqrt x + 1}} = 2 \cr} \)
h) \(\mathop {\lim }\limits_{x \to + \infty } {{1 – 2x + 3{x^3}} \over {{x^3} – 9}} = \mathop {\lim }\limits_{x \to + \infty } {{{1 \over {{x^3}}} – {2 \over {{x^2}}} + 3} \over {1 – {9 \over {{x^3}}}}} = 3\)
i) \(\eqalign{
& \mathop {\lim }\limits_{x \to 0} {1 \over {{x^2}}}\left( {{1 \over {{x^2} + 1}} – 1} \right) \cr
& = \mathop {\lim }\limits_{x \to 0} {1 \over {{x^2}}}.\left( {{{ – {x^2}} \over {{x^2} + 1}}} \right) \cr
& = \mathop {\lim }\limits_{x \to 0} {{ – 1} \over {{x^2} + 1}} = – 1 \cr} \)
j) \(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } {{\left( {{x^2} – 1} \right){{\left( {1 – 2x} \right)}^5}} \over {{x^7} + x + 3}} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{{x^2}\left( {1 – {1 \over {{x^2}}}} \right).{x^5}{{\left( {{1 \over x} – 2} \right)}^5}} \over {{x^7} + x + 3}} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{\left( {1 – {1 \over {{x^2}}}} \right){{\left( {{1 \over x} – 2} \right)}^5}} \over {1 + {1 \over {{x^6}}} + {3 \over {{x^7}}}}} \cr
& = {\left( { – 2} \right)^5} = – 32 \cr}\)
Bài 2.7: Tính giới hạn của các hàm số sau khi \(x \to + \infty \) và khi \(x \to – \infty \)
a) \(f\left( x \right) = {{\sqrt {{x^2} – 3x} } \over {x + 2}}\) ;
b) \(f\left( x \right) = x + \sqrt {{x^2} – x + 1}\) ;
Advertisements (Quảng cáo)
c) \(f\left( x \right) = \sqrt {{x^2} – x} – \sqrt {{x^2} + 1} \) .
a) Khi \(x \to + \infty \)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} – 3x} } \over {x + 2}} = \mathop {\lim }\limits_{x \to + \infty } {{\left| x \right|\sqrt {1 – {3 \over x}} } \over {x + 2}} \cr
& = \mathop {\lim }\limits_{x \to + \infty } {{x\sqrt {1 – {3 \over x}} } \over {x + 2}} = \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {1 – {3 \over x}} } \over {1 + {2 \over x}}} = 1 \cr} \)
Khi \(x \to – \infty \)
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } {{\sqrt {{x^2} – 3x} } \over {x + 2}} = \mathop {\lim }\limits_{x \to – \infty } {{\left| x \right|\sqrt {1 – {3 \over x}} } \over {x + 2}} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{ – x\sqrt {1 – {3 \over x}} } \over {x + 2}} = \mathop {\lim }\limits_{x \to – \infty } {{ – \sqrt {1 – {3 \over x}} } \over {1 + {2 \over x}}} = – 1 \cr}\) ;
b) Khi \(x \to + \infty \)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } \left( {x + \sqrt {{x^2} – x + 1} } \right) \cr
& = \mathop {\lim }\limits_{x \to + \infty } \left( {x + x\sqrt {1 – {1 \over x} + {1 \over {{x^2}}}} } \right) \cr
& = \mathop {\lim }\limits_{x \to + \infty } x\left( {1 + \sqrt {1 – {1 \over x} + {1 \over {{x^2}}}} } \right) = + \infty \cr} \)
Khi \(x \to – \infty \)
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } \left( {x + \sqrt {{x^2} – x + 1} } \right) \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{{x^2} – \left( {{x^2} – 1 + 1} \right)} \over {x – \sqrt {{x^2} – x + 1} }} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{x – 1} \over {x – \sqrt {{x^2} – x + 1} }} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{x – 1} \over {x – \left| x \right|\sqrt {1 – {1 \over x} + {1 \over {{x^2}}}} }} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{x – 1} \over {x + x\sqrt {1 – {1 \over x} + {1 \over {{x^2}}}} }} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{1 – {1 \over x}} \over {1 + \sqrt {1 – {1 \over x} + {1 \over {{x^2}}}} }} = {1 \over 2} \cr} \)
c) Khi \(x \to + \infty \)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right) \cr
& = \mathop {\lim }\limits_{x \to + \infty } {{\left( {{x^2} – x} \right) – \left( {{x^2} + 1} \right)} \over {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} }} \cr
& = \mathop {\lim }\limits_{x \to + \infty } {{ – x – 1} \over {x\sqrt {1 – {1 \over x}} + x\sqrt {1 + {1 \over {{x^2}}}} }} \cr
& = \mathop {\lim }\limits_{x \to + \infty } {{ – 1 – {1 \over x}} \over {\sqrt {1 – {1 \over x}} + \sqrt {1 + {1 \over {{x^2}}}} }} = {{ – 1} \over 2}; \cr} \)
Khi \(x \to – \infty \)
\(\eqalign{
& \mathop {\lim }\limits_{x \to – \infty } \left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right) \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{\left( {{x^2} – x} \right) – \left( {{x^2} + 1} \right)} \over {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} }} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{ – x – 1} \over { – x\sqrt {1 – {1 \over x}} – x\sqrt {1 + {1 \over {{x^2}}}} }} \cr
& = \mathop {\lim }\limits_{x \to – \infty } {{ – 1 – {1 \over x}} \over { – \sqrt {1 – {1 \over x}} – \sqrt {1 + {1 \over {{x^2}}}} }} = {1 \over 2} \cr}\)
Bài 2.8: Cho hàm số \(f\left( x \right) = {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}}\) có đồ thị như hình 4
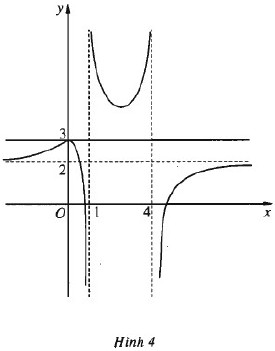
a) Dựa vào đồ thị, dự đoán giới hạn của hàm \(f\left( x \right)\) số khi \(x \to {1^ + }{\rm{ }};{\rm{ }}x \to {1^ – }{\rm{ }};{\rm{ }}x \to {4^ + }{\rm{ }};{\rm{ }}x \to {4^ – }{\rm{ }};{\rm{ }}x \to + \infty {\rm{ }};{\rm{ }}x \to – \infty \)
b) Chứng minh dự đoán trên.
a) Dự đoán :
\(\eqalign{
& \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty {\rm{ ; }}\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = – \infty {\rm{ ; }}\mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right) = – \infty {\rm{ ;}} \cr
& {\rm{ }}\mathop {\lim }\limits_{x \to {4^ – }} f\left( x \right) = + \infty {\rm{ ;}}\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2{\rm{ ; }}\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = 2. \cr} \)
b) Ta có
\(\mathop {\lim }\limits_{x \to {1^ + }} \left( {2{x^2} – 15x + 12} \right) = – 1 < 0,{\rm{ }}\mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} – 5x + 4} \right) = 0\)
và \({x^2} – 5x + 4 < 0\) với mọi \(x \in \left( {1;4} \right)\) nên \(\mathop {\lim }\limits_{x \to {1^ + }} {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}} = + \infty \)
Vì \(\eqalign{
& \mathop {\lim }\limits_{x \to {1^ – }} \left( {2{x^2} – 15x + 12} \right) = – 1 < 0, \cr
& \mathop {\lim }\limits_{x \to {1^ – }} \left( {{x^2} – 5x + 4} \right) = 0 \cr} \)
và \({x^2} – 5x + 4 > 0\) với mọi x < 1 nên \(\mathop {\lim }\limits_{x \to {1^ – }} {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}} = – \infty \)
Vì \(\eqalign{
& \mathop {\lim }\limits_{x \to {4^ + }} \left( {2{x^2} – 15x + 12} \right) = – 16 < 0, \cr
& \mathop {\lim }\limits_{x \to {4^ + }} \left( {{x^2} – 5x + 4} \right) = 0 \cr} \)
và \({x^2} – 5x + 4 > 0\) với mọi x > 4 nên \(\mathop {\lim }\limits_{x \to {4^ + }} {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}} = – \infty \)
Vì
\(\eqalign{
& \mathop {\lim }\limits_{x \to {4^ – }} \left( {2{x^2} – 15x + 12} \right) = – 16 < 0, \cr
& \mathop {\lim }\limits_{x \to {4^ – }} \left( {{x^2} – 5x + 4} \right) = 0 \cr} \)
và \({x^2} – 5x + 4 < 0\) với mọi \(x \in \left( {1;4} \right)\) nên \(\mathop {\lim }\limits_{x \to {4^ – }} {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}} = + \infty\) ;
\(\mathop {\lim }\limits_{x \to + \infty } {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}} = \mathop {\lim }\limits_{x \to + \infty } {{2 – {{15} \over x} + {{12} \over {{x^2}}}} \over {1 – {5 \over x} + {4 \over {{x^2}}}}} = 2\)
\(\mathop {\lim }\limits_{x \to – \infty } {{2{x^2} – 15x + 12} \over {{x^2} – 5x + 4}} = \mathop {\lim }\limits_{x \to – \infty } {{2 – {{15} \over x} + {{12} \over {{x^2}}}} \over {1 – {5 \over x} + {4 \over {{x^2}}}}} = 2\)

