Bài 1.5: Xác định tính chẵn lẻ của các hàm số
a) \(y = {{\cos 2x} \over x}\)
b) \(y = x – \sin x\)
c) \(y = \sqrt {1 – \cos x} \)
d) \(y = 1 + \cos x\sin \left( {{{3\pi } \over 2} – 2x} \right)\)
a) \(y = {{\cos 2x} \over x}\) là hàm số lẻ
b) \(y = x – \sin x\) là hàm số lẻ
c) \(y = \sqrt {1 – \cos x} \) là hàm số chẵn
d) \(y = 1 + \cos x\sin \left( {{{3\pi } \over 2} – 2x} \right)\) là hàm số chắn
Bài 1.6: a) Chứng minh rằng \(\cos 2\left( {x + k\pi } \right) = \cos 2x,k \in Z\) . Từ đó vẽ đồ thị hàm số y = cos 2x
b) Từ đồ thị hàm số y = cos 2x, hãy vẽ đồ thị hàm số y = |cos 2x|
Advertisements (Quảng cáo)
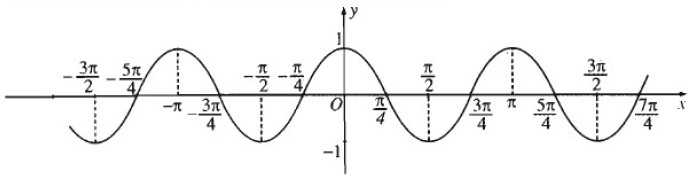
a) \(\cos 2(x + k\pi ) = \cos (2x + k2\pi ) = \cos 2x,k \in Z\). Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos 2x
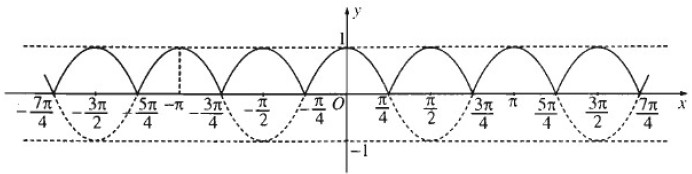
b) Đồ thị hàm số y = |cos 2x|
Advertisements (Quảng cáo)
Bài 1.7: Hãy vẽ đồ thị của các hàm số
a) y = 1 + sin x
b) y = cos x – 1
c) \(y = \sin \left( {x – {\pi \over 3}} \right)\)
d) \(y = \cos \left( {x + {\pi \over 6}} \right)\)
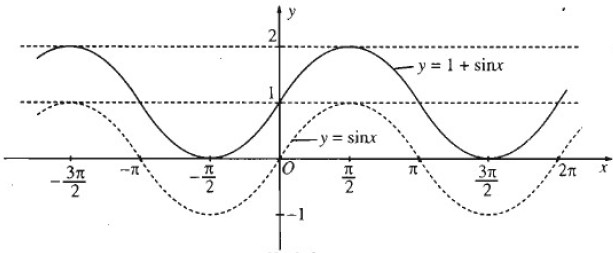
a) Đồ thị hàm số y = 1 + sin x thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục tung lên phía trên một đơn vị.
b) Đồ thị hàm số y = cos x – 1 thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục tung xuống phía dưới một đơn vị.
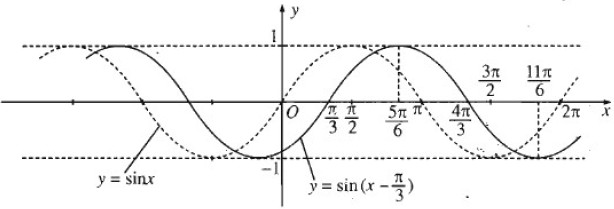
c) Đồ thị hàm số \(y = \sin \left( {x – {\pi \over 3}} \right)\) thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \({\pi \over 3}\)
d) Đồ thị hàm số \(y = \cos \left( {x + {\pi \over 6}} \right)\) thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng \({\pi \over 6}\)
Bài 1.8: Hãy vẽ đồ thị của các hàm số
a) \(y = \tan \left( {x + {\pi \over 4}} \right)\)
b) \(y = \cot \left( {x – {\pi \over 6}} \right)\)
a) Đồ thị hàm số \(y = \tan \left( {x + {\pi \over 4}} \right)\) thu được từ đồ thị hàm số y = tanx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng \({\pi \over 4}\).
b) Đồ thị hàm số \(y = \cot \left( {x – {\pi \over 6}} \right)\) thu được từ đồ thị hàm số y = cotx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \({\pi \over 6}\)
