Bài 1.13: Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội \(q = {2 \over 3}\)
ĐS: \({u_n} = {\left( {{2 \over 3}} \right)^{n – 1}}\)
Bài 1.14: Cho dãy số \(\left( {{b_n}} \right)\) có số hạng tổng quát là \({b_n} = \sin \alpha + {\sin ^2}\alpha + … + {\sin ^n}\alpha \) với \(\alpha \ne {\pi \over 2} + k\pi \). Tìm giới hạn của \(\left( {{b_n}} \right)\)
Dãy số: \(\sin \alpha ,…,{\sin ^n}\alpha ,…\) với \(\alpha \ne {\pi \over 2} + k\pi \), là một cấp số nhân vô hạn, công bội \(q = \sin \alpha \)
Vì \(\left| {\sin \alpha } \right| < 1\) với \(\alpha \ne {\pi \over 2} + k\pi \) nên \(\left( {{{\sin }^n}\alpha } \right)\) là một cấp số nhân lùi vô hạn.
Hơn nữa, \({b_n} = \sin \alpha + {\sin ^2}\alpha + … + {\sin ^n}\alpha = {S_n}\)
Do đó, \(\lim {b_n} = \sin \alpha + {\sin ^2}\alpha + … + {\sin ^n}\alpha + … = {{\sin \alpha } \over {1 – \sin \alpha }}\)
Bài 1.15: Cho số thập phân vô hạn tuần hoàn a = 34,121212… (chu kì là 12). Hãy viết a dưới dạng một phân số.
Advertisements (Quảng cáo)
Giải tương tự Ví dụ 13, ta có \(a = 34,121212… = {{1126} \over {33}}\)
Bài 1.16: Giả sử ABC là tam giác vuông cân tại A với độ dài cạnh góc vuông bằng 1. Ta tạo ra các hình vuông theo các bước sau đây :
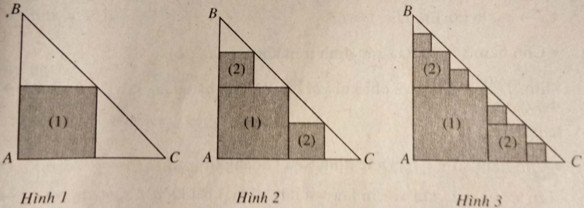
– Bước 1: Dựng hình vuông màu xám có mộtđỉnhA, ba đỉnh còn lại là các trung điểm của ba cạnhAB, BC và AC (H.1). Kí hiệu hình vuông này là (1).
– Bước2 : Với 2 tam giác vuông cân màu trắng còn lại như trong hình 1, ta lại tạo được 2 hình vuông màu xám khác theo cách trên, kí hiệu là (2) (H.2).
– Bước 3: Với 4 tam giác vuông cân màu trắng như trong hình 2, ta lại tạo được 4 hình vuông mới màu xámtheo cách trên (H.3).
– …
Advertisements (Quảng cáo)
– Bước thứ n :Ở bước này ta có \({2^{n – 1}}\) hình vuông mới màu xám được tạo thành theo cách trên, kí hiệu là (n)
a) Gọi \({u_n}\) là tổng diện tích của tất cả các hình vuông mới được tạo thành ở bước thứ n. Chứng minh rằng \({u_n} = {1 \over {{2^{n + 1}}}}\)
b) Gọi \({S_n}\) là tổng diện tích của tất cả các hình vuông màu xám có được sau n bước. Quan sát hình vẽ để dự đoán giới hạn của \({S_n}\) khi \(n \to + \infty \). Chứng minh dự đoán đó.
a) Chứng minh bằng quy nạp \({u_n} = {1 \over {{2^{n + 1}}}}\) (1)
– Với n = 1, một hình vuông được tạo thành có diện tích là \({u_1} = {1 \over {{2^2}}}\)
Vậy (1) đúng.
– Giả sử công thức (1) đúng với \(n = k\left( {k \ge 1} \right)\) nghĩa là \({u_k} = {1 \over {{2^{k + 1}}}}\). Ta cần chứng minh (1) đúng với \(n = k + 1\) tức là chứng minh \({u_{k + 1}} = {1 \over {{2^{k + 2}}}}\)
Thật vậy, ở bước thứ k ta có \({2^{k – 1}}\) hình vuông mới màu xám được tạo thành.Ứng với mỗi hình vuông này ta lại tạo được hai hình vuông mới trong bước thứ k + 1
Tổng diện tích của hai hình vuông mới nàytrong bước thứ k + 1 bằng nửa diện tích của hình vuông tương ứng bước thứ k
Do đó, tổng diện tích tất cả các hình vuông mới có được trong bước thứ k + 1 là \({u_{k + 1}} = {1 \over 2}.{1 \over {{2^{k + 1}}}} = {1 \over {{2^{k + 2}}}}\) Vậy (1) đúng với n = k + 1
– Kết luận: Với mọi n nguyên dương ta luôn có \({u_n} = {1 \over {{2^{n + 1}}}}\)
b) Dự đoán : \({S_n} \to {1 \over 2}{S_{ABC}}\) khi \(n \to + \infty \) hay \(\lim {S_n} = {1 \over 2}\)
Chứng minh :
\(\eqalign{
& {S_n} = {u_1} + {u_2} + … + {u_n} \cr
& = {1 \over {{2^2}}} + {1 \over {{2^3}}} + … + {1 \over {{2^{n + 1}}}} \cr
& = {1 \over 2} – {1 \over {{2^{n + 1}}}} \cr}\)
Từ đó suy ra \(\lim {S_n} = {1 \over 2}\)

