Bài 36: Giải và biện luận các bất phương trình:
a) mx+4 > 2x+m2
b) 2mx+1 ≥ x+4m2
c) x(m2-1) < m4-1
d) 2(m+1)x ≤ (m+1)2(x-1)
Đáp án
a) Ta có:
mx + 4 > 2x + m2 ⇔ (m – 2)x > m2 – 4
+ Nếu m > 2 thì \(S = (m + 2, +∞)\)
+ Nếu m < 2 thì \(S = (-∞; m + 2)\)
+ Nếu m = 2 thì \(S = Ø\)
b) Ta có:
\(2mx+1 ≥ x+4m^2⇔ (2m – 1)x ≥ 4m^2– 1\)
+ Nếu \(m > {1 \over 2}\) thì \(S = [2m +1; +∞)\)
+ Nếu \(m < {1 \over 2}\) thì \(S = (-∞; 2m + 1]\)
+ Nếu \(m = {1 \over 2}\) thì \(S =\mathbb R\)
c) x(m2-1) < m4-1
+ Nếu m2 – 1 > 0 ⇔ m < -1 hoặc m > 1 thì \(S = (-∞, m^2+ 1)\)
+ Nếu m2 – 1 < 0 ⇔ -1 < m < 1 thì \(S = (m^2+1, +∞)\)
+ Nếu \(m = ±1\) thì \(S = Ø\)
d) \(2\left( {m + 1} \right)x{\rm{ }} \le {\rm{ }}{\left( {m + 1} \right)^2}\left( {x – 1} \right){\rm{ }} \)
\(\Leftrightarrow {\rm{ }}({m^2}-{\rm{ }}1)x{\rm{ }} \ge {\rm{ }}{\left( {m{\rm{ }} + {\rm{ }}1} \right)^2}\)
Advertisements (Quảng cáo)
+ Nếu m2 – 1 > 0 ⇔ m < -1 hoặc m > 1 thì \(S = {\rm{[}}{{m + 1} \over {m – 1}}; + \infty )\)
+ Nếu m2 -1 < 0 ⇔ -1 < m < 1 thì \(S = ( – \infty ;{{m + 1} \over {m – 1}}{\rm{]}}\)
+ Nếu \(m = -1\) thì \(S =\mathbb R\)
+ Nếu \(m = 1\) thì \(0x ≥ 4; S = Ø\)
Bài 37: Giải các bất phương trình sau:
a) \(( – \sqrt 3 x + 2)(x + 1)(4x – 5) > 0\)
b) \({{3 – 2x} \over {(3x – 1)(x – 4)}} < 0\)
c) \({{ – 3x + 1} \over {2x + 1}} \le – 2\)
d) \({{x + 2} \over {3x + 1}} \le {{x – 2} \over {2x – 1}}\)
Đáp án
a) Ta có bảng xét dấu:
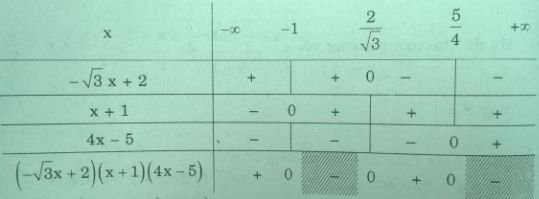
Vậy \(S = ( – \infty , – 1) \cup ({2 \over {\sqrt 3 }};{5 \over 4})\)
b) Ta có bảng xét dấu:
Advertisements (Quảng cáo)

Vậy \(S = ({1 \over 3};{3 \over 2}) \cup (4, + \infty )\)
c) Ta có:
\(\eqalign{
& {{ – 3x + 1} \over {2x + 1}} \le – 2 \Leftrightarrow {{ – 3x + 1 + 2(2x + 1)} \over {2x + 1}} \le 0 \cr
& \Leftrightarrow {{x + 3} \over {2x + 1}} \le 0 \Leftrightarrow – 3 \le x < – {1 \over 2} \cr} \)
Vậy \(S = {\rm{[ – 3,}}-{1 \over 2})\)
d) Ta có:
\(\eqalign{
& {{x + 2} \over {3x + 1}} \le {{x – 2} \over {2x – 1}} \cr&\Leftrightarrow {{(x + 2)(2x – 1) – (x – 2)(3x + 1)} \over {(3x + 1)(2x – 1)}} \le 0 \cr
& \Leftrightarrow {{ – {x^2} + 8x} \over {(3x + 1)(2x – 1)}} \le 0\cr& \Leftrightarrow {{x(x – 8)} \over {(3x + 1)(2x – 1)}} \ge 0 \cr} \)
Lập bảng xét dấu vế trái

Vậy tập nghiệm của bất phương trình là:\(S = ( – \infty ; – {1 \over 3}) \cup {\rm{[}}0,{1 \over 2}) \cup {\rm{[}}8, + \infty )\)
Bài 38: Giải và biện luận các bất phương trình
a) \((2x – \sqrt 2 )(x – m) > 0\)
b) \({{\sqrt 3 – x} \over {x – 2m + 1}} \le 0\)
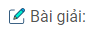
Ta có:
\(\eqalign{
& (2x – \sqrt 2 ) = 0 \Leftrightarrow x = {{\sqrt 2 } \over 2} \cr
& x – m = 0 \Leftrightarrow x = m \cr} \)
i) Với \(x < {{\sqrt 2 } \over 2}\) , ta có bảng xét dấu:
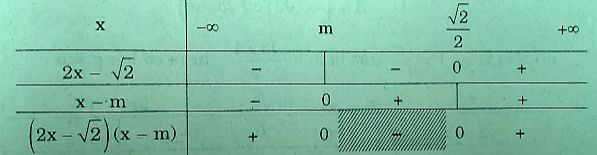
Vậy \(S = ( – \infty ;m) \cup ({{\sqrt 2 } \over 2}, + \infty )\)
ii) Với \(m = {{\sqrt 2 } \over 2}\) thì bất phương trình trở thành:
\(\eqalign{
& (2x – \sqrt 2 )(x – {{\sqrt 2 } \over 2}) > 0 \Leftrightarrow {(2x – \sqrt 2 )^2} > 0 \cr
& \Leftrightarrow x \ne {{\sqrt 2 } \over 2} \cr
& S = R\backslash {\rm{\{ }}{{\sqrt 2 } \over 2}{\rm{\} }} \cr} \)
iii) Với \(m > {{\sqrt 2 } \over 2}\) , ta có bảng xét dấu:
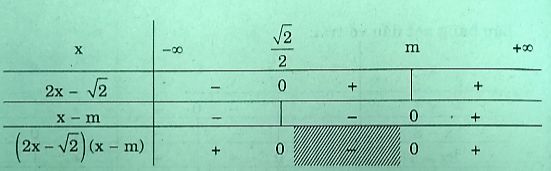
\(S = ( – \infty ;{{\sqrt 2 } \over 2}) \cup (m; + \infty )\)
b) Ta có:
\(\eqalign{
& \sqrt 3 – x = 0 \Leftrightarrow x = \sqrt 3 \cr
& x – 2m + 1 = 0 \Leftrightarrow x = 2m – 1 \cr} \)
i) Nếu \(2m – 1 < \sqrt 3 \Leftrightarrow m < {{\sqrt 3 + 1} \over 2}\) , ta có bảng sau:

\(S = \left( { – \infty ;2m – 1} \right) \cup \left[ {\sqrt 3 ; + \infty } \right)\)
ii) Nếu \(2m – 1 = \sqrt 3 \Leftrightarrow m = {{\sqrt 3 + 1} \over 2}\) thì dễ thấy tập nghiệm là:
\(S = ( – \infty ,\sqrt 3 ) \cup (\sqrt 3 , + \infty )\)
iii) Nếu \(2m – 1 > \sqrt 3 \Leftrightarrow m > {{\sqrt 3 + 1} \over 2}\) thì ta có bảng sau:
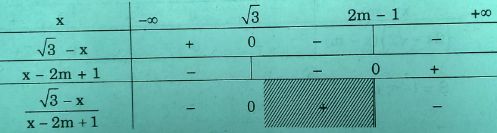
Vậy tập nghiệm là \(S = ( – \infty ,\sqrt 3 ) \cup (2m – 1; + \infty )\)

