Bài 1: Cho tam giác \(ABC\). Gọi \(A’, B’, C’\) lần lượt là trung điểm các cạnh \(BC, CA, AB\). Vectơ \(\overrightarrow {{A’}{B’}} \) cùng hướng với vectơ nào trong các vectơ sau đây ?
(A) \(\overrightarrow {AB} \) ; (B) \(\overrightarrow {A{C’}} \) ;
(C) \(\overrightarrow {BA} \) ; (D) \(\overrightarrow {{C’}B} \) .

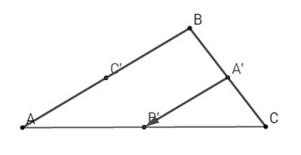
Chọn (C).
Bài 2: Cho ba điểm \(M, N, P\) thẳng hàng, trong đó điểm \(N\) nằm giữa hai điểm \(M\) và \(P\) . Khi đó các cặp vec tơ nào sau đây cùng hướng ?
(A) \(\overrightarrow {MN} \) và \(\overrightarrow {PN} \) ;
(B) \(\overrightarrow {MN} \) và \(\overrightarrow {MP} \) ;
(C) \(\overrightarrow {MP} \) và \(\overrightarrow {PN} \) ;
Advertisements (Quảng cáo)
(D) \(\overrightarrow {NM} \) và \(\overrightarrow {NP}\) .

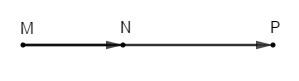
Chọn (B).
Bài 3: Cho hình chữ nhật \(ABCD.\) Trong các đẳng thức dưới đây, đẳng thức nào đúng ?
(A) \(\overrightarrow {AB} = \overrightarrow {CD} \) ;
Advertisements (Quảng cáo)
(B) \(\overrightarrow {BC} = \overrightarrow {DA} \) ;
(C) \(\overrightarrow {AC} = \overrightarrow {BD} \) ;
(D) \(\overrightarrow {AD} = \overrightarrow {BC} \).

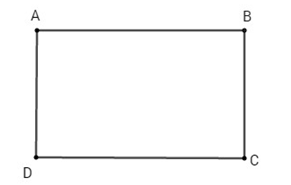
Chọn (D).
Bài 4: Cho tam giác đều \(ABC\) với đường cao \(AH\). Đẳng thức nào dưới đây đúng ?
(A) \(\overrightarrow {HB} = \overrightarrow {HC} \) ;
(B) \(\overrightarrow {AC} = 2\overrightarrow {HC} \) ;
(C) \(\left| {\overrightarrow {AH} } \right| = {{\sqrt 3 } \over 2}\left| {\overrightarrow {BC} } \right|\) ;
(D) \(\overrightarrow {AB} = \overrightarrow {AC} \).

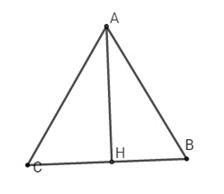
Đường cao tam giác đều cạnh \(a\) có độ dài bằng \({{a\sqrt 3 } \over 2}\).
Chọn (C).

