Bài 1.19: Trong mặt phẳng Oxy, cho \(\overrightarrow v = \left( {2;0} \right)\) và điểm M(1; 1).
a) Tìm tọa độ của điểm M’ là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ \(\overrightarrow v \)
b) Tìm tọa độ của điểm M” là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow v \) và phép đối xứng qua trục Oy.
a) M(-1;1) đối xứng qua trục Oy ta được N(-1;1).
Gọi M'(x;y) là ảnh của N(-1;1) qua phép tịnh tiến theo vecto \(\vec v(2;0)\)
\( \Rightarrow \left\{ \matrix{
x = – 1 + 2 = 1 \hfill \cr
y = 1 + 0 = 1 \hfill \cr} \right. \Rightarrow M’ \equiv M(1;1)\)
b) Gọi P(x;y) là ảnh của \(M(1;1)\) qua phép tịnh tiến theo \(\vec v(2;0)\)
\( \Rightarrow \left\{ \matrix{
x = 1 + 2 = 3 \hfill \cr
y = 1 + 0 = 1 \hfill \cr} \right. \Rightarrow P(3;1)\)
P(3;1) đối xứng qua trục Oy ta được M”( – 3;1)
Advertisements (Quảng cáo)
Bài 1.20: Trong mặt phẳng Oxy, cho vectơ \(\overrightarrow v = \left( {3;1} \right)\) và đường thẳng d có phương trình \(2x – y = 0\). Tìm ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc 90° và phép tịnh tiến theo vectơ \(\overrightarrow v \).
Gọi \(d_1\) là ảnh của d qua phép quay tâm 0 góc 90°. Vì d chứa tâm quay O nên \(d_1\) cũng chứa O. Ngoài ra \(d_1\) vuông góc với d nên \(d_1\) có phương trình \9x + 2y = 0\).
Gọi d’ là ảnh của \(d_1\) qua phép tịnh tiến vectơ (\overrightarrow v \). Khi đó phương trình của d’ có dạng \(x + 2y + C = 0\). Vì d’ chứa \(O’\left( {3;1} \right)\) là ảnh của O qua phép tịnh tiến vectơ (\overrightarrow v \) nên \(3 + 2 + C = 0\) từ đó C = -5. Vậy phương trình của d’ là \(x + 2y – 5 = 0\).
Bài 1.21: Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.
Advertisements (Quảng cáo)
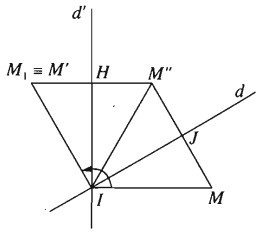
Gọi \({Q_{\left( {I,\alpha } \right)}}\) là phép quay tâm I góc \(\alpha \) . Lấy đường thẳng d bất kì qua I. Gọi d’ là ảnh của d qua phép quay tâm I góc \({\alpha \over 2}\). Lấy điểm M bất kì và gọi \(M’ = {Q_{\left( {I,\alpha } \right)}}\left( M \right)\). Gọi M” là ảnh của M qua phép đối xứng qua trục d. \(M_1\) là ảnh của M” qua phép đối xứng qua trục d’. Gọi J là giao của MM” với d, H là giao của \(M”{M_1}\) với d’. Khi đó ta có đẳng thức giữa các góc lượng giác sau:
\(\eqalign{
& \left( {IM,I{M_1}} \right) = \left( {IM,IM”} \right) + \left( {IM”,I{M_1}} \right) \cr
& = 2\left( {IJ,IM”} \right) + 2\left( {IM”,IH} \right) \cr
& = 2\left( {IJ,IH} \right) \cr
& = 2{\alpha \over 2} = a = \left( {IM,IM’} \right) \cr} \)
Từ đó suy ra \(M’ \equiv {M_1}\). Như vậy M’ có thể xem là ảnh của sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục d và d’.
Bài 1.22: Cho hình vuông ABCD có tâm I. Trên tia BC lấy điểm E sao cho BE = AI.
a) Xác định một phép dời hình biến A thành B và I thành E
b) Dựng ảnh của hình vuông ABCD qua phép dời hình ấy.
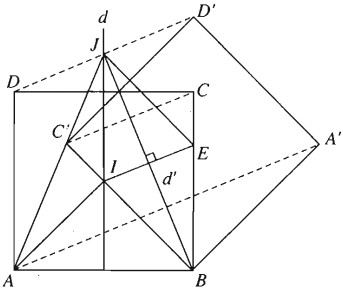
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d’ của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d’, thì dễ thấy \(J{\rm{A}} = JB,JI = J{\rm{E}}\) và \(2\left( {JI,JB} \right) = \left( {JI,J{\rm{E}}} \right) = {45^0}\)
(vì \(JE\parallel IB\)). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc 45°
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A’, D’, C’. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA’D’C’ đối xứng với hình vuông BADC qua d’

