Bài 1.35: Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
Tập hợp các điểm N thuộc đường tròn (C’) là ảnh của (C) qua phép đối xứng qua trung điểm của AB.
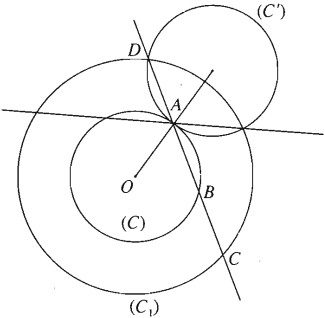
Bài 1.36: Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và \(r,\left( {R > r} \right)\). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho \(CD = 3AB\).
Advertisements (Quảng cáo)
Gọi (C) là đường tròn tâm O bán kính r, \((C_1)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng tâm A. Gọi (C’) là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C’) và \((C_1)\). Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C’) với \((C_1)\).
Bài 1.37: Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x + y – 2 = 0\). Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc 45°.
Advertisements (Quảng cáo)
Dễ thấy d chứa điểm \(H\left( {1;1} \right)\) và \(OH \bot d\). Gọi H’ là ảnh của H qua phép quay tâm O góc 45° thì \(H’ = \left( {0;\sqrt 2 } \right)\). Từ đó suy ra d’ phải qua H’ và vuông góc với OH’. Vậy phương trình của d’ là \(y = \sqrt 2 \).
Bài 1.38: Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng 60°. Chứng minh rằng tứ giác MNPQ là một hình thang cân.
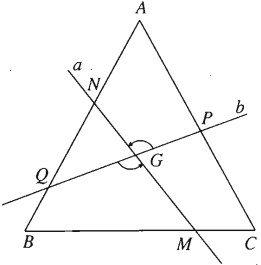
Gọi \({Q_{\left( {G;{{120}^0}} \right)}}\) là phép quay tâm G góc \(120^0\). Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.
Tương tự \({Q_{\left( {G;{{120}^0}} \right)}}\) cũng biến Q thành M. Từ đó suy ra \(GP = GN,GQ = GM\). Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì \({Q_{\left( {G;{{120}^0}} \right)}}\) biến PQ thành NM nên \(PQ = NM\). Từ đó suy ra hai tam giác \(NQM\) và \(PMQ\) bằng nhau. Do đó \(\widehat {NQM} = \widehat {PMQ}\). Tương tự \(\widehat {QNP} = \widehat {MPN}\).
Từ đó suy ra \(\widehat {PNQ} + \widehat {NQM} = {180^0}\)
Do đó \(NP\parallel QM\). Vậy ta có tứ giác \(MPNQ\) là hình thang cân.

