Bài 1.39: Gọi A’, B’, C’ tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng: \(\overrightarrow {A’B’} .\overrightarrow {A’C’} = {k^2}\overrightarrow {AB.} \overrightarrow {AC} \)
Theo định nghĩa của phép đồng dạng ta có \(B’C’ = kBC\), từ đó suy ra \(B’C{‘^2} = {k^2}B{C^2}\). Hay $${\left( {\overrightarrow {A’C’} – \overrightarrow {A’B’} } \right)^2} = {k^2}{\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right)^2}\). Suy ra
\(A’C{‘^2} – 2\overrightarrow {A’C’} .\overrightarrow {A’B’} + A’B{‘^2}\)
\(= {k^2}\left( {A{C^2} – 2\overrightarrow {AC} .\overrightarrow {AB} + A{B^2}} \right)\).
Để ý rằng \(A’C{‘^2} = {k^2}A{C^2},A’B{‘^2} = {k^2}A{B^2}\) ta suy ra điều phải chứng minh.
Bài 1.40: Gọi A’, B’ và C’ tương ứng là ảnh của ba điểmA, B và C qua phép đồng dạng. Chứng minh rằng \(\overrightarrow {AB} = p\overrightarrow {AC} \) nếu $$\overrightarrow {A’B’} = p\overrightarrow {A’C’} \) thì , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B’ nằm giữa hai điểm A’ và C’.
Advertisements (Quảng cáo)
Để ý rằng
\(\eqalign{
& A’C{‘^2} = {k^2}A{C^2},A’B{‘^2} \cr
& = {k^2}A{B^2},\overrightarrow {A’C’} .\overrightarrow {A’B’} \cr
& = {k^2}\overrightarrow {AC} .\overrightarrow {AB} \cr} \)
Ta có:
\({\left( {\overrightarrow {A’B’} – p\overrightarrow {A’C’} } \right)^2} = A’B{‘^2} – 2p\overrightarrow {A’B’} .\overrightarrow {A’C’} + {p^2}A’C{‘^2}\)
\(\eqalign{
& = {k^2}\left( {A{B^2} – 2p\overrightarrow {AB} .\overrightarrow {AC} + {p^2}A{C^2}} \right) \cr
& = {k^2}{\left( {\overrightarrow {AB} – p\overleftarrow {AC} } \right)^2} = 0 \cr} \)
Advertisements (Quảng cáo)
Từ đó suy ra \(\overrightarrow {A’B’} – p\overrightarrow {A’C’} = \overrightarrow 0 \)
Giả sử ba điểm \(A,B,C\) thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó \(\overrightarrow {AB} = t\overrightarrow {AC} \), với \(0 < t < 1\). Áp dụng bài 1.39 ta cũng có \(\overrightarrow {A’B} = t\overrightarrow {A’C’} \), với \(0 < t < 1\). Do đó ba điểm \(A’,B’,C’\) thẳng hàng và điểm B’ nằm giữa hai điểm A’ và C’.
Bài 1.41: Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm \(M\left( {x;y} \right)\) thành \(M’\left( {2{\rm{x}} – 1; – 2y + 3} \right)\). Chứng minh F là một phép đồng dạng.
Lấy điểm \(N\left( {{x_1};{y_1}} \right)\), thì điểm \(N’\left( {2{x_1} – 1; – 2{y_1} + 3} \right) = F\left( N \right)\). Ta có
\(\eqalign{
& M’N{‘^2} = {\left( {2{{\rm{x}}_1} – 2{\rm{x}}} \right)^2} + {\left( { – 2{y_1} + 2y} \right)^2} \cr
& = 4\left[ {{{\left( {{x_1} – x} \right)}^2} + {{\left( {{y_1} – y} \right)}^2}} \right] = 4M{N^2} \cr} \)
Từ đó suy ra với hai điểm M, N tùy ý và M’, N’ lần lượt là ảnh của chúng qua F ta có \(M’N’ = 2MN\). Vậy F là phép đồng dạng với tỉ số đồng dạng là 2.
Bài 1.42: Dựng tam giác BAC vuông cân tại A có C là một điểm cho trước, còn hai đỉnh A, B lần lượt thuộc hai đường thẳng a, b song song với nhau cho trước.
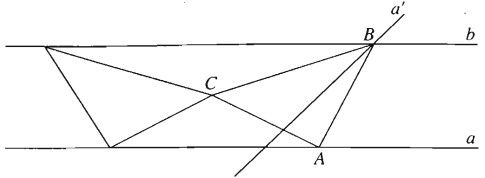
Xem B là ảnh của A qua phép đồng dạng có được bằng cách thực hiện liên tiếp phéo quay tâm C góc \( \pm {45^0}\) và phép vị tự tâm C tỉ số \(k = \sqrt 2 \). Vì A thuộc a nên B thuộc đường thẳng a’ là ảnh của a qua phép đồng dạng nói trên. Vậy b là giao của a’ và b. Từ đó suy ra cách dựng . Bài toán có hai nghiệm hình.

