Bài 1.23: Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình \(2x + y – 4 = 0\).
a) Hãy viết phương trình của đường thẳng d1 là ảnh của d qua phép vị tự tâm O tỉ số k = 3
b) Hãy viết phương trình của đường thẳng d2 là ảnh của d qua phép vị tự tâm I(1; 2) tỉ số k = -2
a) Lấy hai điểm \(A\left( {0;4} \right)\) và \(B\left( {2;0} \right)\) thuộc d. Gọi \(A’,B’\) theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có
\(\overrightarrow {OA’} = 3\overrightarrow {OA} ,\overrightarrow {OB’} = 3\overrightarrow {OB} \).
Vì \(\overrightarrow {OA} = \left( {0;4} \right)\) nên \(\overrightarrow {OA’} = \left( {0;12} \right)\). Do đó \(A’ = \left( {0;12} \right)\). Tương tự \(B’ = \left( {6;0} \right)\); \(d_1\) chính là đường thẳng A’B’ nên nó có phương trình
\({{x – 6} \over { – 6}} = {y \over {12}}\) hay \(2{\rm{x}} + y – 12 = 0\).
b) Có thể giải tương tự như câu a) . Sau đây ta sẽ giải bằng cách khác.
Vì \({d_2}\parallel d\) nên phương trình của \(d_2\) có dạng \(2{\rm{x}} + y + C = 0\): . Gọi \(A’ = \left( {x’;y’} \right)\) là ảnh của A qua phép vị tự đó thì ta có:
\(\overrightarrow {IA’} = – 2\overrightarrow {IA} \) hay \(x’ + 1 = – 2,y’ – 2 = – 4\)
Suy ra \(x’ = – 3,y’ = – 2\)
Advertisements (Quảng cáo)
Do A’ thuộc \(d_2\) nên \(2.\left( { – 3} \right) – 2 + C = 0\). Từ đó suy ra C = 8
Phương trình của \(d_2\) là \(2{\rm{x}} + y + 8 = 0\)
Bài 1.24: Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình
\({\left( {x – 3} \right)^2} + {\left( {y + 1} \right)^2} = 9\) .
Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1; 2) tỉ số k = -2
Ta có \(A\left( {3; – 1} \right)\) là tâm của (C) nên tâm A’ của (C’) là ảnh của A qua phép vị tự đã cho. Từ đó suy ra \(A’ = \left( { – 3;8} \right)\). Vì bán kính của (C) bằng 3, nên bán kính của (C’) bằng \(\left| { – 2} \right|.3 = 6\)
Vậy (C’) có phương trình : \({\left( {x + 3} \right)^2} + {\left( {y – 8} \right)^2} = 36\).
Advertisements (Quảng cáo)
Bài 1.25: Cho nửa đường tròn đường kính AB. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính AB của nửa đường tròn đó.
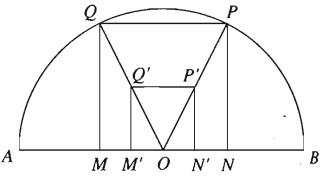
Gọi O là trung điểm của AB. Giả sử dựng được hình vuông MNPQ có M, N thuộc đường kính AB; P, Q thuộc nửa đường tròn. Khi đó O phải là trung điểm của MN. Nếu lấy một hình vuông M’N’P’Q’ sao cho M’, N’ thuộc AB, O là trung điểm của M’N’ thì dễ thấy
\({{OM} \over {OM’}} = {{ON} \over {ON’}} = {{OP} \over {OP’}} = {{OQ} \over {OQ’}}\)
Từ đó suy ra hình vuông MNPQ là ảnh của hình vuông M’N’P’Q’ qua phép vị tự tâm O, suy ra O, P, P’ và O, Q, Q’ thẳng hàng. Vậy ta có cách dựng:
– Dựng hình vuông M’N’P’Q’ nằm trong nửa hình tròn đã cho sao cho M’N’ thuộc AB và O là trung điểm của M’N’. Tia OP’ cắt nửa đường tròn tại P; tia OQ’ cắt nửa đường tròn tại Q.
Khi đó dễ thấy tứ giác MNPQ là hình vuông cần dựng
Bài 1.26: Cho góc nhọn xOy và điểm C nằm trong góc đó. Tìm trên Oy điểm A sao cho khoảng cách từ A đến Ox bằng AC.
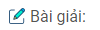
Giả sử điểm A đã dựng được . Gọi B là hình chiếu vuông góc của A trên Ox, khi đó AB = AC. Lấy điểm A’ bất kì trên Oy, gọi B’ là hình chiếu vuông góc của A’ trên Ox, đường thẳng qua A’ song song với AC cắt đường thẳng OC tại C’. Khi đó có thể coi tam giác ABC là ảnh của tam giác A’B’C’ qua phép vị tự tâm O tỉ số \({{AC} \over {A’C’}}\) nên A’C’ = A’B’.
Từ đó suy ra cách dựng:
– Lấy điểm A bất kì trên Oy, dựng B’ là hình chiếu vuông góc của A lên Ox
– Lấy C’ là một giao điểm của đường tròn tâm A’ bán kính A’B’ với đường thẳng OC.
– Đường thẳng qua C song song với A’C’ cắt Oy tại A.
Dễ thấy A là điểm phải dựng.
Bài toán có hai nghiệm hình.

