Câu 78: Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC.
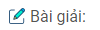
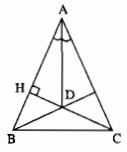
∆ABC cân tại A, đường phân giác của góc ở đỉnh cũng là đường cao.
Do đó:
\(\eqalign{
& A{\rm{D}} \bot BC \cr
& CH \bot AB\left( {gt} \right) \cr} \)
Trong ∆ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC, do đó BD là đường cao xuất phát từ đỉnh B đến cạnh đối diện AC.
Vậy \(B{\rm{D}} \bot AC\).
Câu 79: Cho tam giác ABC có AB = AC = 13cm, BC = 10cm. Tính độ dài đường trung tuyến AM.
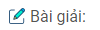
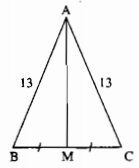
∆ABC cân tại A nên đường trung tuyến AM cũng là đường cao.
\( \Rightarrow AM \bot BC\)
\(MB = MC = {1 \over 2}BC = 5\left( {cm} \right)\)
Trong tam giác vuông AMB có \(\widehat {AMB} = 90^\circ \)
Theo định lý Pytago ta có:
\(A{B^2} = A{M^2} + M{B^2}\)
Advertisements (Quảng cáo)
\(\eqalign{
& \Rightarrow A{M^2} = A{B^2} – M{B^2} = {15^2} – {5^2} \cr
& = 169 – 25 = 144 \Rightarrow AM = 12\left( {cm} \right) \cr} \)
Câu 80: Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn, AC < AB. Kẻ đường cao AH. Chứng minh rằng \(\widehat {AHB} < \widehat {HAC}\).
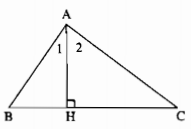
Trong ∆ABC ta có: AC > AB
\(\Rightarrow \widehat B > \widehat C\) (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat {{A_1}} = 90^\circ \) (tính chất tam giác vuông) (1)
Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)
\( \Rightarrow \widehat C + \widehat {{A_2}} = 90^\circ \) (tính chất tam giác vuông) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: \(\widehat B + \widehat {{A_1}} = \widehat C + \widehat {{A_2}}\)
Mà \(\widehat B > \widehat C\) nên \(\widehat {{A_1}} < \widehat {{A_2}}\)
Câu 81: Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (hình dưới)
a) Chứng minh rằng A là trung điểm EF.
b) Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
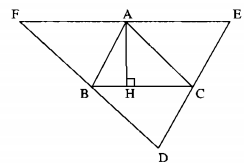
a) Xét ∆ABC và ∆ACE:
\(\widehat {ACB} = \widehat {CA{\rm{E}}}\) (so le trong, AE // BC)
AC cạnh chung
\(\widehat {CAB} = \widehat {AC{\rm{E}}}\) (so le trong, CE // AB)
Do đó: ∆ABC = ∆CEA (g.c.g)
\( \Rightarrow \) AE = BC (1)
Xét ∆ABC và ∆ABF:
\(\widehat {ABC} = \widehat {{\rm{BAF}}}\) (so le trong, BF // AC)
AC cạnh chung
\(\widehat {BAC} = \widehat {ABF}\) (so le trong, BF // AC)
Do đó: ∆ABC = ∆BAF (g.c.g)
\( \Rightarrow \) AF = BC (2)
Từ (1) và (2) suy ra: AE = AF. Vậy A là trung điểm EF.
b) Kẻ \({\rm{A}}H \bot BC\)
EF // BC (gt)
\( \Rightarrow \) \(AH \bot EF\)
AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Chứng minh tương tự câu a, ta có B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ∆ABC là đường trung trực DFF.
Ta có C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ∆ABC là đường trung trực của DE.

